FDS Review | mio的博客

Algorithm Anlysis

Space Comlexity

The space complexity of an algorithm or a computer program is the amount of memory space required to solve an instance of the computational problem as a function of characteristics of the input. It is the memory required by an algorithm until it executes completely.

Time Comlexity

In computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by the algorithm, supposing that each elementary operation takes a fixed amount of time to perform. Thus, the amount of time taken and the number of elementary operations performed by the algorithm are taken to be related by a constant factor.

List

Abustrct Data Type

【Definition】
An Abstract Data Type (ADT) is a data type that is organized in such a way that the specification on the objects and specification of the operations on the objects are separated from the representation of the objects and the implementation on the operations.

Linked List

Interfaces

#ifndef LLIST_H
#define LLIST_H

typedef void node_proc_fun_t(void*);
typedef int node_comp_fun_t(const void*, const void*);

typedef void LLIST_T;

LLIST_T *llist_new(int elmsize);
int llist_delete(LLIST_T *ptr);

int llist_node_append(LLIST_T *ptr, const void *datap);
int llist_node_prepend(LLIST_T *ptr, const void *datap);

int llist_travel(LLIST_T *ptr, node_proc_fun_t *proc);

void llist_node_delete(LLIST_T *ptr, node_comp_fun_t *comp, const void *key); 
void *llist_node_find(LLIST_T *ptr, node_comp_fun_t *comp, const void *key);

#endif

Stack & Queue

Stack

Definition

【Definition】
A stack is a Last-In-First-Out (LIFO) list, that is, an ordered list in which insertions and deletions are made at the top only.

Operations & Implementations
Operations:
Int  IsEmpty( Stack S );
Stack CreateStack(); 
DisposeStack( Stack S ); //该函数销毁数组栈(释放数组空间与栈空间)，返回NULL指针
MakeEmpty( Stack S ); 
Push( ElementType X, Stack S ); 
ElementType Top( Stack S ); 
Pop( Stack S );
Array Implementation:
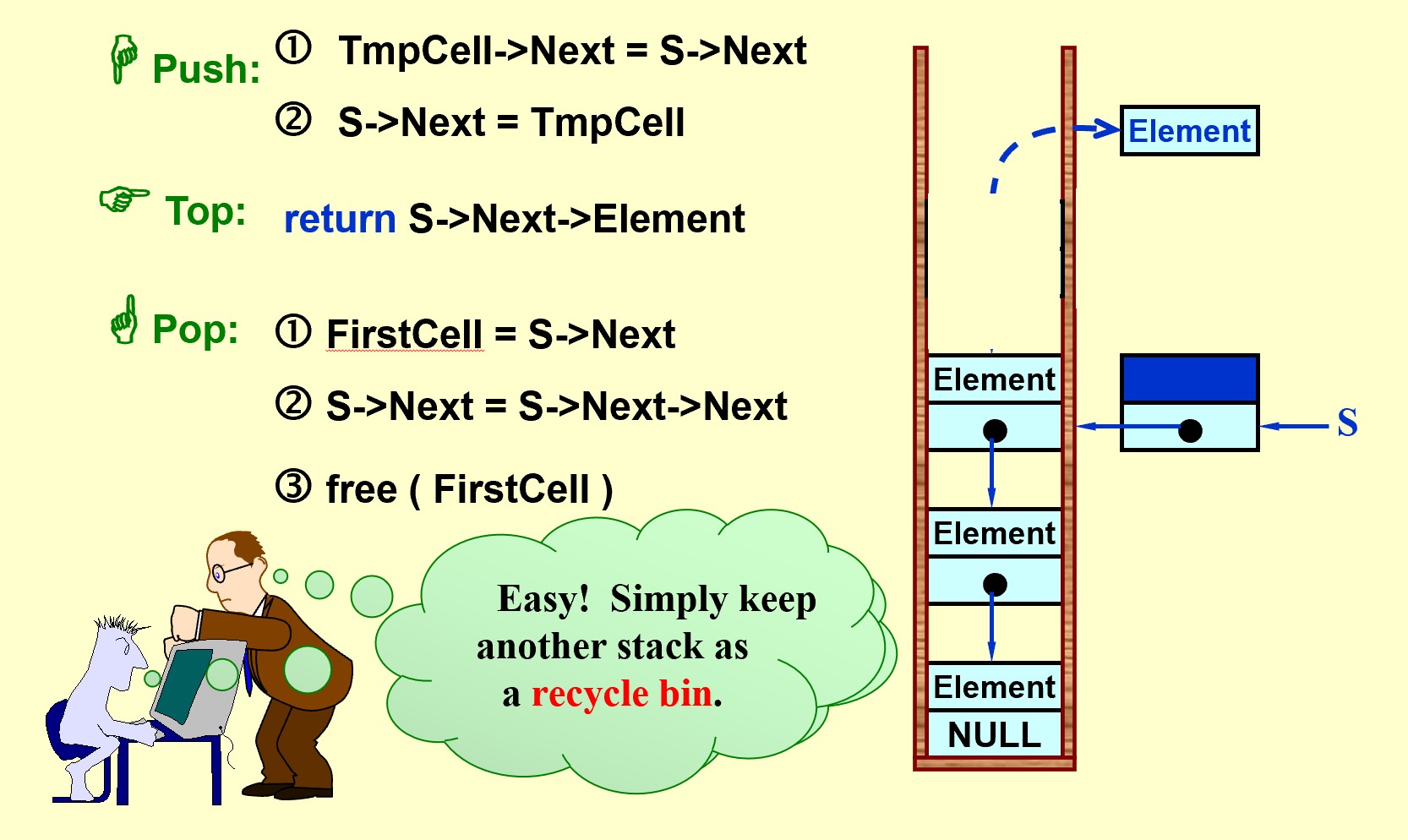
struct  StackRecord {
    int Capacity ;              /* size of stack */
    int TopOfStack;          /* the top pointer */
    /* ++ for push, -- for pop, -1 for empty stack */
    ElementType *Array;    /* array for stack elements */
 } ;
Linked List Implemetation(with Dummy):

Applications

Balance Symbols

Algorithm {
    Make an empty stack S;
    while(read in a character c) {
        if(c is an opening symbol)
            Push(c, S);
        else if(c is a closing symbol) {
            if(S is empty)  { ERROR; exit; }
            else{  /* stack is okay */
                if (Top(S) doesn’t match c)  { ERROR, exit; }
                else Pop(S);
            }  /* end else-stack is okay */
        }  /* end else-if-closing symbol */
    } /* end while-loop */ 
    if (S is not empty)  ERROR;
}

Postfix Infix Prefix Evaluation

Note:

The order of operands is the same in infix and postfix.
Operators with higher precedence appear before those with lower precedence.

With () Implementation:

Never pop a ( from the stack except when processing a ) .
Observe that when ( is not in the stack, its precedence is the highest; but when it is in the stack, its precedence is the lowest. Define in-stack precedence and incoming precedence for symbols, and each time use the corresponding precedence for comparison.
括号入栈前优先级最高，入栈后优先级最低。
Plz read DS03 PPT Page 7 for further.

Queue
Definition
【Definition】
A queue is a First-In-First-Out (FIFO) list, that is, an ordered list in which insertions take place at one end and deletions take place at the opposite end.

Operations & Implementations
Operations:
```
int IsEmpty( Queue Q );
Queue CreateQueue( ); 
DisposeQueue( Queue Q ); 
MakeEmpty( Queue Q ); 
Enqueue( ElementType X, Queue Q ); 
ElementType  Front( Queue Q ); 
Dequeue( Queue Q );
```
Implementations:
```
struct  QueueRecord {
 int Capacity ;   /* max size of queue */
 int Front;          /* the front pointer */
 int Rear;           /* the rear pointer */
 int Size;  /* Optional - the current size of queue */
 ElementType *Array;    /* array for queue elements */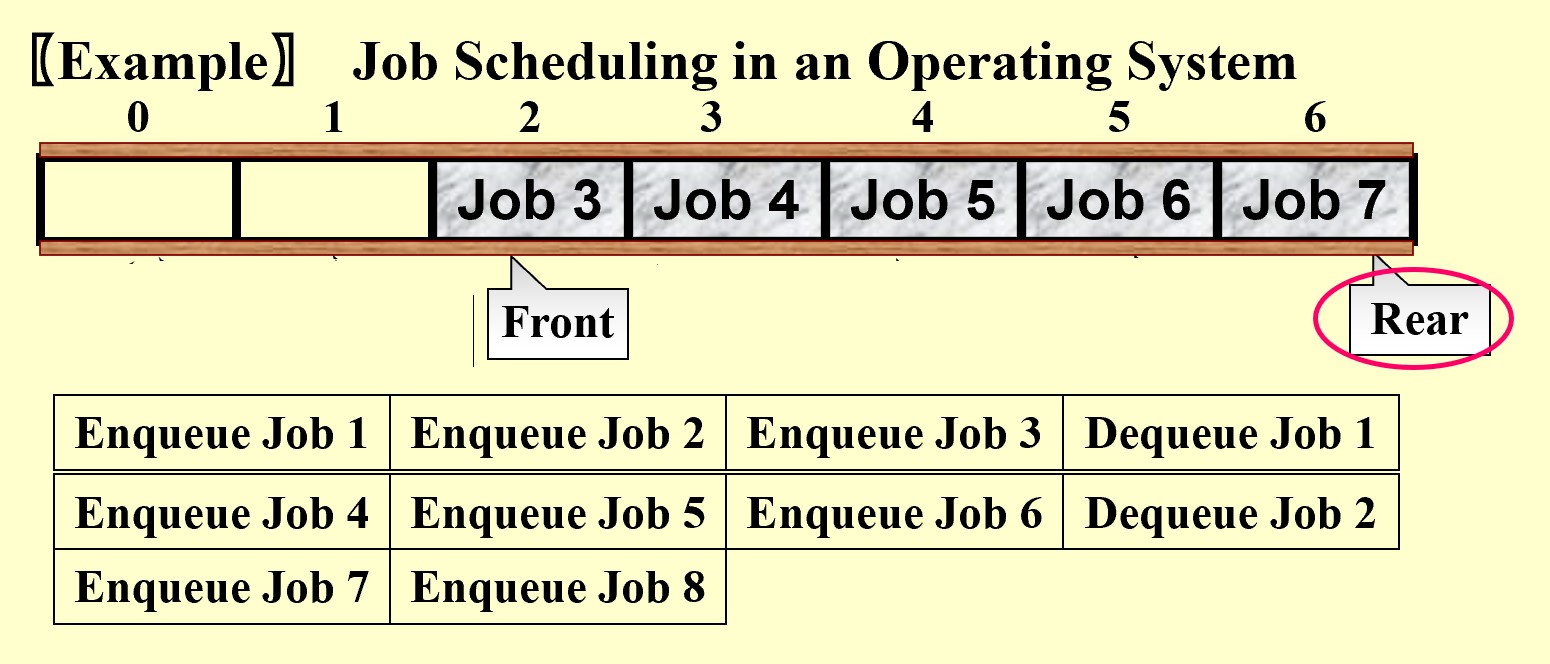
} ;
```
Learn more about queue plz read PPT DS03 Page 11

Circular Queue:
队列的入队、出队操作很简单。入队时，通过rear的位置判断队列是否已满。如果没有满，则将rear后移一位，将新元素放置在rear所在位置。出队时，也可以通过rear的位置判断队列是否为空。如果不空，则只需将front后移一位即可。获取队头元素，判断队列不空，则只需返回front指向位置的元素即可。

想像一下，通过出队操作将数据弹出队列后，front之前的空间还能够再次得到吗？不能。所以使用普通数组实现队列，就再也不能使用front之前的空间了，这会导致大量空间丢失。

为了解决这个问题，将普通数组换成循环数组。在循环数组中，末尾元素的下一个元素不是数组外，而是数组的头元素。这样就能够再次使用front之前的存储空间了。

为了规避环形队列的两种边界情况：空或者满时都有rear-front=1,我们让两者始终差1，即始终有一个空位。

Complete Binary Tree and Heap

Operations and Implementations

Operations

PriorityQueue  Initialize( int MaxElements ); 
void  Insert( ElementType X, PriorityQueue H ); 
ElementType  DeleteMin( PriorityQueue H ); 
ElementType  FindMin( PriorityQueue H );

Simple Implementations

Binary Heap

Definition

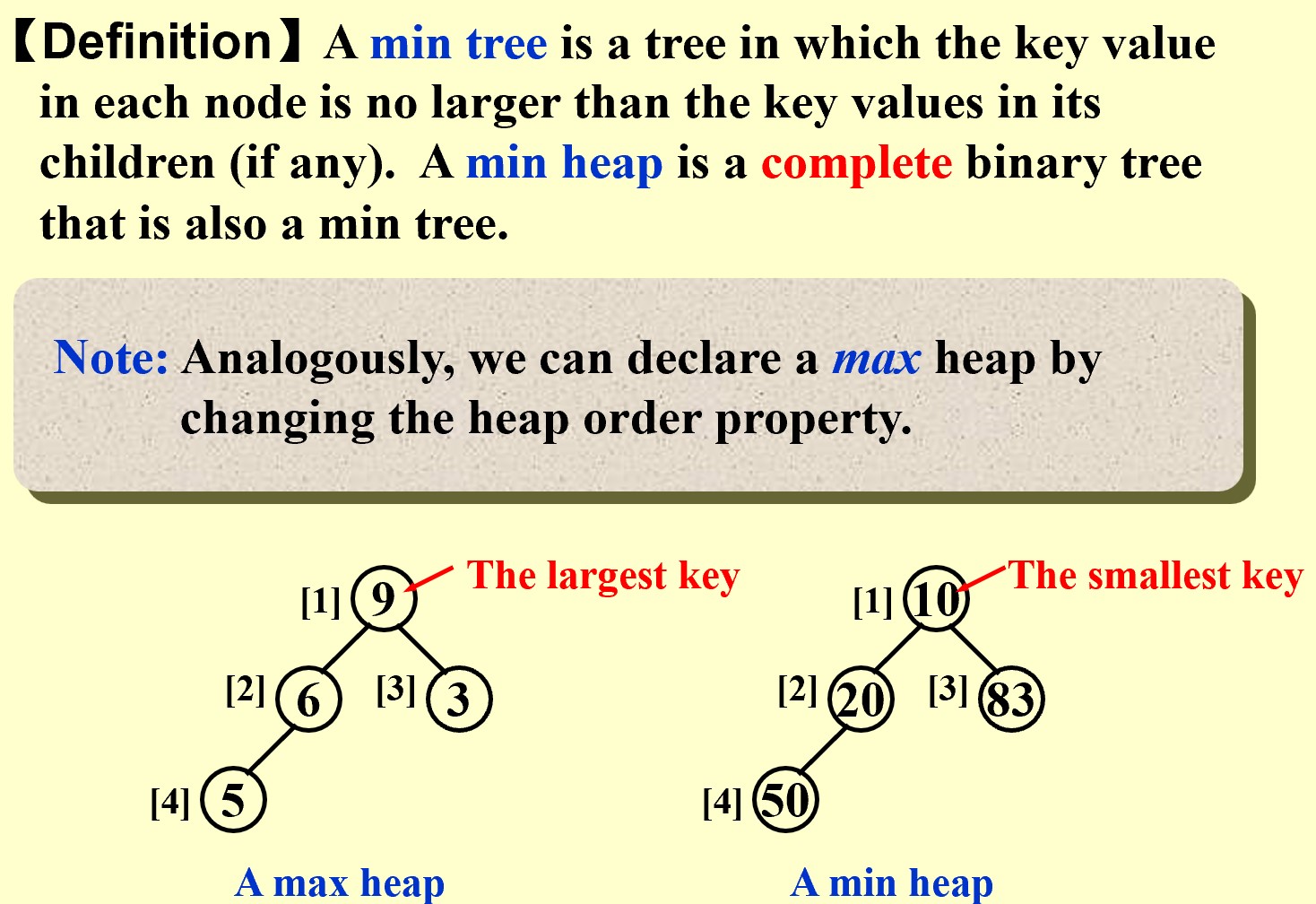
【Definition】
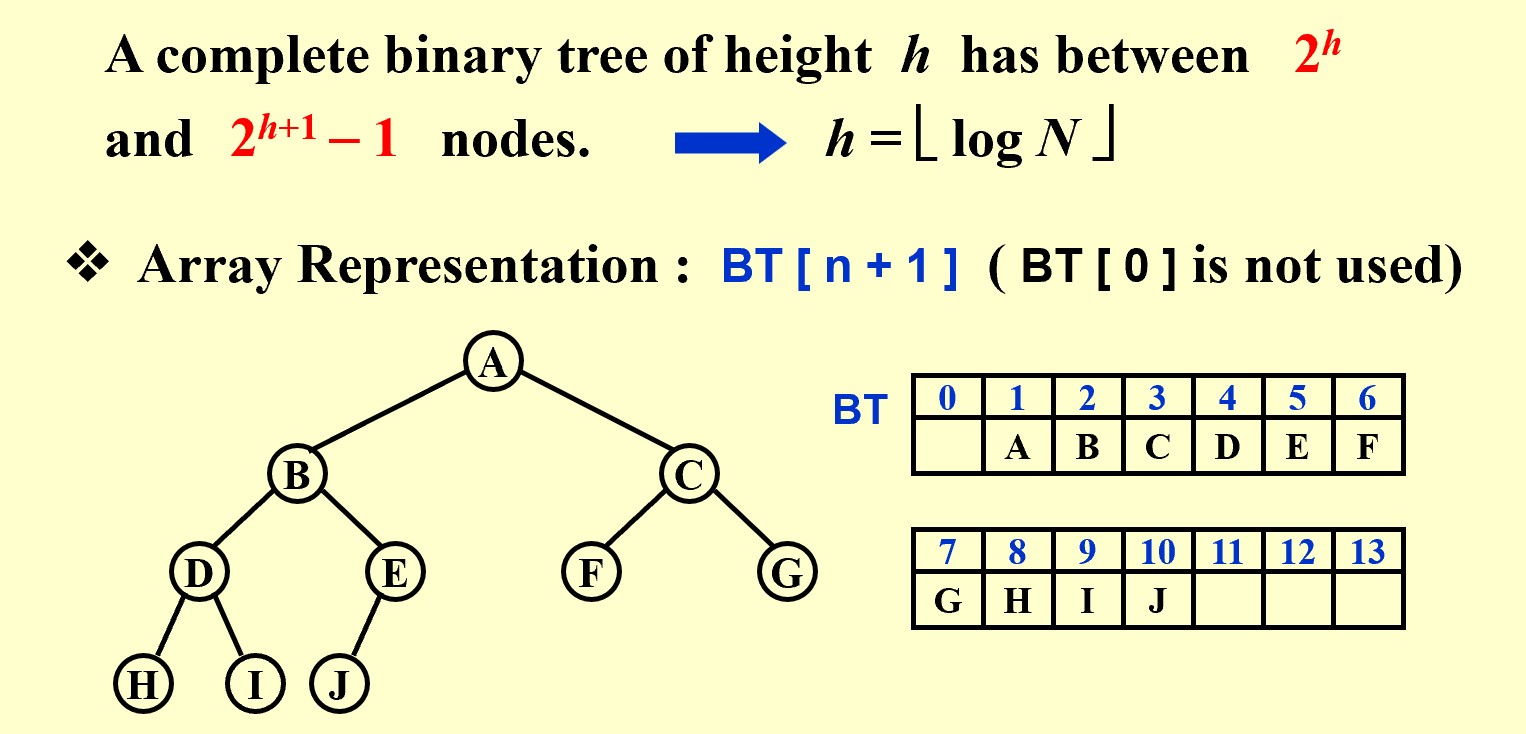
A binary tree with n nodes and height h is complete iff its nodes correspond to the nodes numbered from 1 to n in the perfect binary tree of height h.

也就是说，叶子节点只可能在最大的两层出现，上一层不满不可能有下一层。

Array Representation

MinHeap & MaxHeap

Implementations

Initialize

PriorityQueue Initialize( int  MaxElements ) 
{ 
     PriorityQueue  H; 
     if ( MaxElements < MinPQSize ) 
    return  Error( "Priority queue size is too small" ); 
     H = malloc( sizeof ( struct HeapStruct ) ); 
     if ( H ==NULL ) 
    return  FatalError( "Out of space!!!" ); 
     /* Allocate the array plus one extra for sentinel */ 
     H->Elements = malloc(( MaxElements + 1 ) * sizeof( ElementType )); 
     if ( H->Elements == NULL ) 
    return  FatalError( "Out of space!!!" ); 
     H->Capacity = MaxElements; 
     H->Size = 0; 
     H->Elements[ 0 ] = MinData;  /* set the sentinel */
     return  H; 
}

Insert

/* H->Element[ 0 ] is a sentinel */ sentinel:dummy
void  Insert( ElementType  X,  PriorityQueue  H ) 
{ 
     int  i; 

     if ( IsFull( H ) ) { 
    Error( "Priority queue is full" ); 
    return; 
     } 

     for ( i = ++H->Size; H->Elements[ i / 2 ] > X; i /= 2 ) 
    H->Elements[ i ] = H->Elements[ i / 2 ]; 

     H->Elements[ i ] = X; 
}

$T (N) = O ( log N )$

DeleteMin

ElementType  DeleteMin( PriorityQueue  H ) 
{ 
    int  i, Child; 
    ElementType  MinElement, LastElement; 
    if ( IsEmpty( H ) ) { 
         Error( "Priority queue is empty" ); 
         return  H->Elements[ 0 ];   } 
    MinElement = H->Elements[ 1 ];  /* save the min element */
    LastElement = H->Elements[ H->Size-- ];  /* take last and reset size */
    for ( i = 1; i * 2 <= H->Size; i = Child ) {  /* Find smaller child */ 
         Child = i * 2; 
         if (Child != H->Size && H->Elements[Child+1] < H->Elements[Child]) 
           Child++;     
         if ( LastElement > H->Elements[ Child ] )   /* Percolate one level */ 
           H->Elements[ i ] = H->Elements[ Child ]; 
         else     break;   /* find the proper position */
    } 
    H->Elements[ i ] = LastElement; 
    return  MinElement; 
}

$T (N) = O ( log N )$

PercolateUp & PercolateDown

void PercolateUp( int p, PriorityQueue H ){
    int i;
    int x=H->Elements[p];
    for(i = p;H->Elements[i/2]>x && i>0;i/=2){
        H->Elements[i]=H->Elements[i/2];
    }
    H->Elements[i]=x;
}

void PercolateDown( int p, PriorityQueue H ){
    int i;
    int child;
    int x=H->Elements[p];
    for(i = p;i*2<=H->Size;i=child){
        child=i*2;
        if(child != H->Size && H->Elements[child+1] < H->Elements[child]){
            child++;
        }
        if(x>H->Elements[child]){
            H->Elements[i]=H->Elements[child];
        }
        else{
            break;
        }
    }
    H->Elements[i]=x;
}

Puzzles

Judgment and Choice

Push 5 characters ooops onto a stack. In how many different ways that we can pop these characters and still obtain ooops?
5

ooo出入栈顺序随意，之后push( p ),pop( p ),push( o ),pop( o )。注意出栈不能比入栈多。
可以入出入出入出，入出入入出出，入入出入出出，入入出出入出，入入入出出出，5个
Suppose that an array of size 6 is used to store a circular queue, and the values of front and rear are 0 and 4, respectively. Now after 2 dequeues and 2 enqueues, what will the values of front and rear be?
```
A.2 and 0
```
Program
7-1 Pop Sequence
Given a stack which can keep M numbers at most. Push N numbers in the order of 1, 2, 3, …, N and pop randomly. You are supposed to tell if a given sequence of numbers is a possible pop sequence of the stack. For example, if M is 5 and N is 7, we can obtain 1, 2, 3, 4, 5, 6, 7 from the stack, but not 3, 2, 1, 7, 5, 6, 4.

Input Specification:
Each input file contains one test case. For each case, the first line contains 3 numbers (all no more than 1000): M (the maximum capacity of the stack), N (the length of push sequence), and K (the number of pop sequences to be checked). Then K lines follow, each contains a pop sequence of N numbers. All the numbers in a line are separated by a space.

Output Specification:
For each pop sequence, print in one line “YES” if it is indeed a possible pop sequence of the stack, or “NO” if not.

Sample Input:

5 7 5
1 2 3 4 5 6 7
3 2 1 7 5 6 4
7 6 5 4 3 2 1
5 6 4 3 7 2 1
1 7 6 5 4 3 2

Solution

#include<stdio.h>
void StackCheck(int m,int n,int a[]){
        int b[1000];
        int top=0,ptr=0,temp=1;
        while (ptr<n) {
            if (temp==a[ptr] && top<m) {
                ptr++;
                temp++;
            }//模拟入栈和给出栈顶的数字相同
            else if(top>0 && b[top]==a[ptr]){
                top--;
                ptr++;
            }//模拟栈顶和给出栈顶的数字相同
            else if(top<m-1 && ptr<n){
                b[++top]=temp;
                temp++;
            }//都不同，模拟入栈
            else{
                break;
            }
        }
        if (ptr<n) printf("NO\n");//不可能的条件
        else printf("YES\n");
}
int main() {
    int m,n,k;
    scanf("%d %d %d",&m,&n,&k);
    for (int i=0; i<k; i++) {
        int a[1000];
        for (int j=0; j<n; j++) {
            scanf("%d",&a[j]);
        }
        StackCheck(m,n,a);
    }
    return 0;
}

Sample Output:

YES
NO
NO
YES
NO

Tree

Definition

【Definition】
A tree is a collection of nodes. The collection can be empty; otherwise, a tree consists of:
(1) a distinguished node r, called the root;
(2) and zero or more nonempty (sub)trees T1, …, Tk, each of whose roots are connected by a directed edge from r.

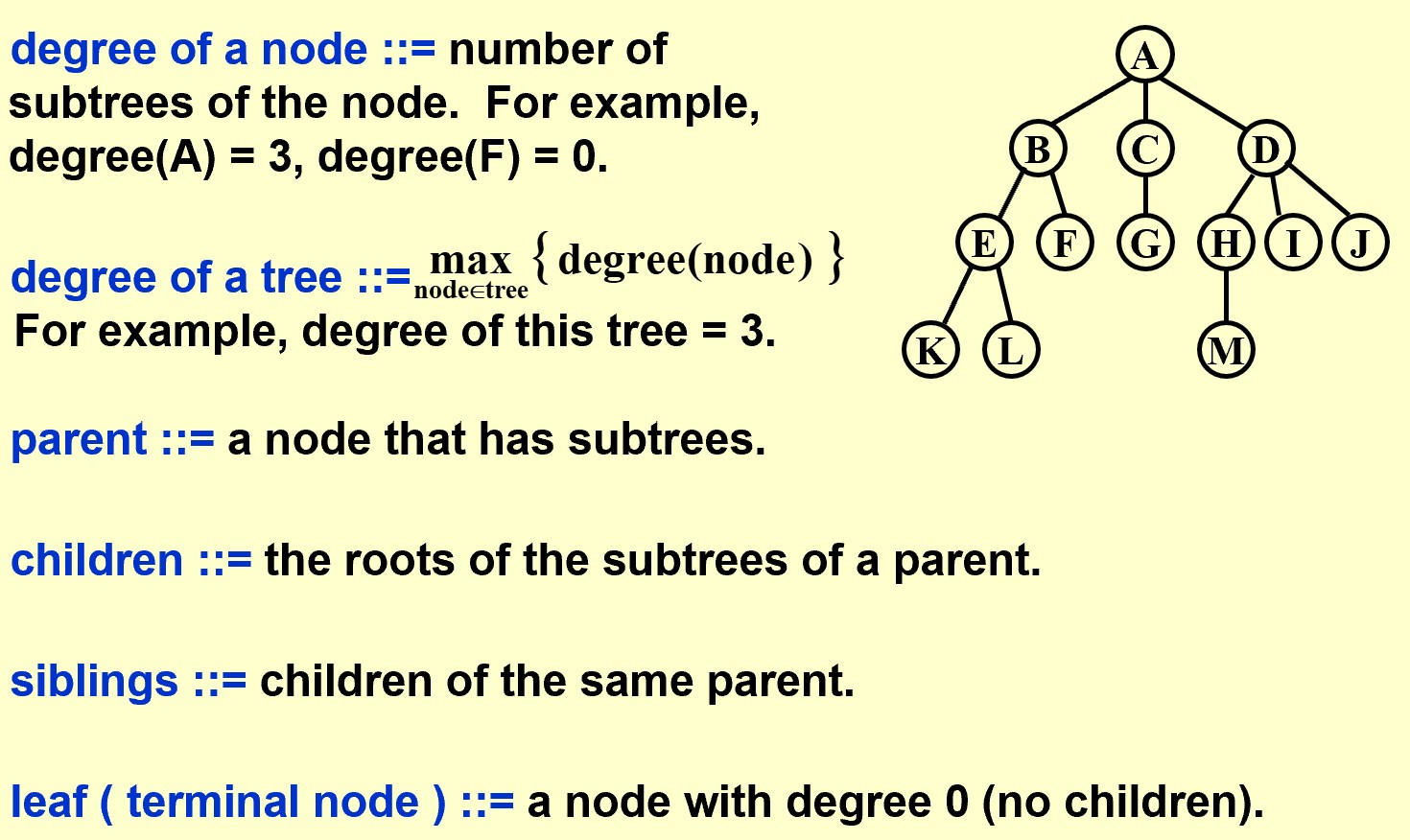
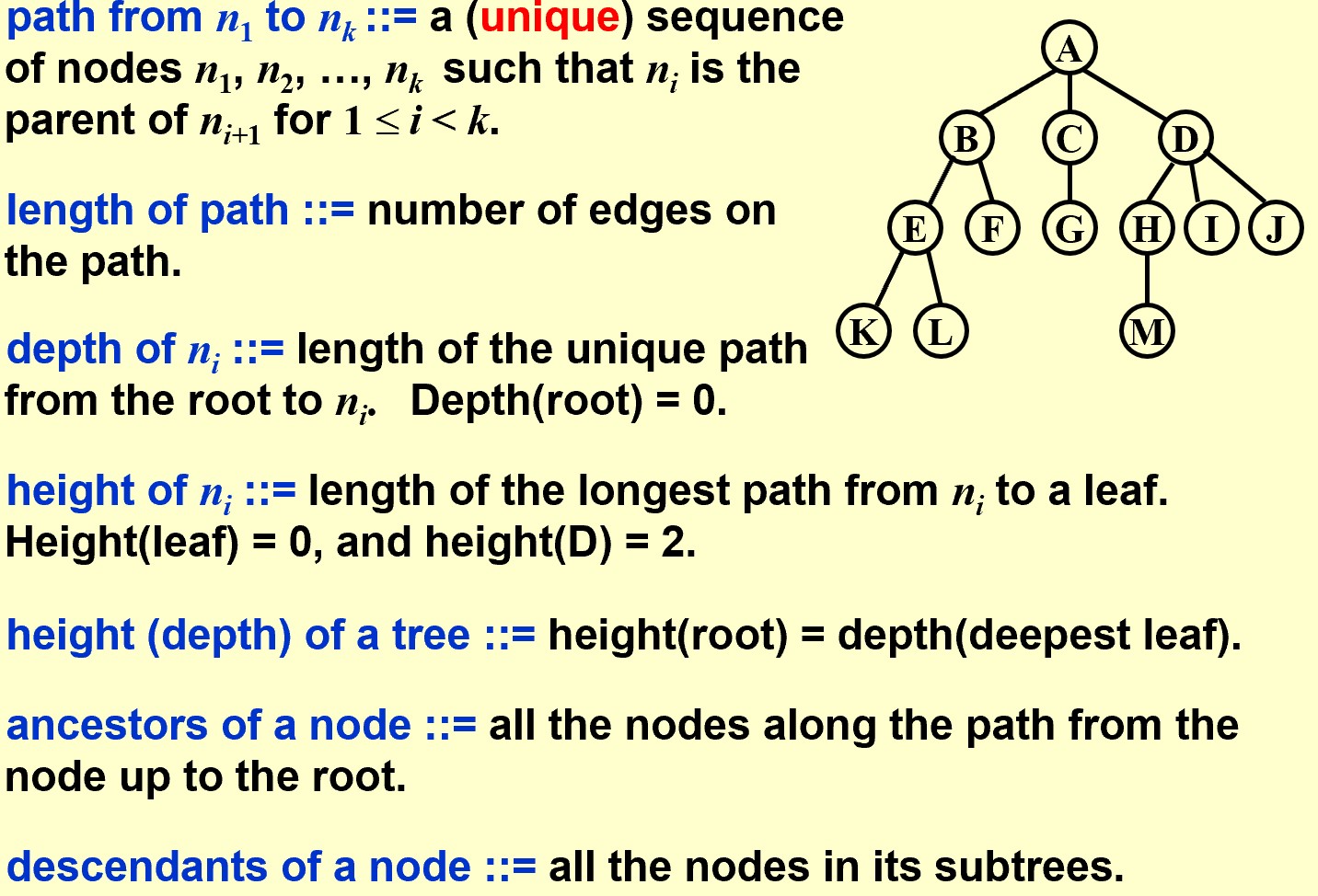
深度：从root算起
高度：从leaf算起

Implementation

Turn to BiTree

First, we need to transfer the tree into a BiTree.
要点：

从这棵树的根结点开始，从上到下，看每一个结点，把你正在看的结点的孩子放在左子树，兄弟放在右子树。

口诀：

将节点的孩子放在左子树；
将节点的兄弟放在右子树。

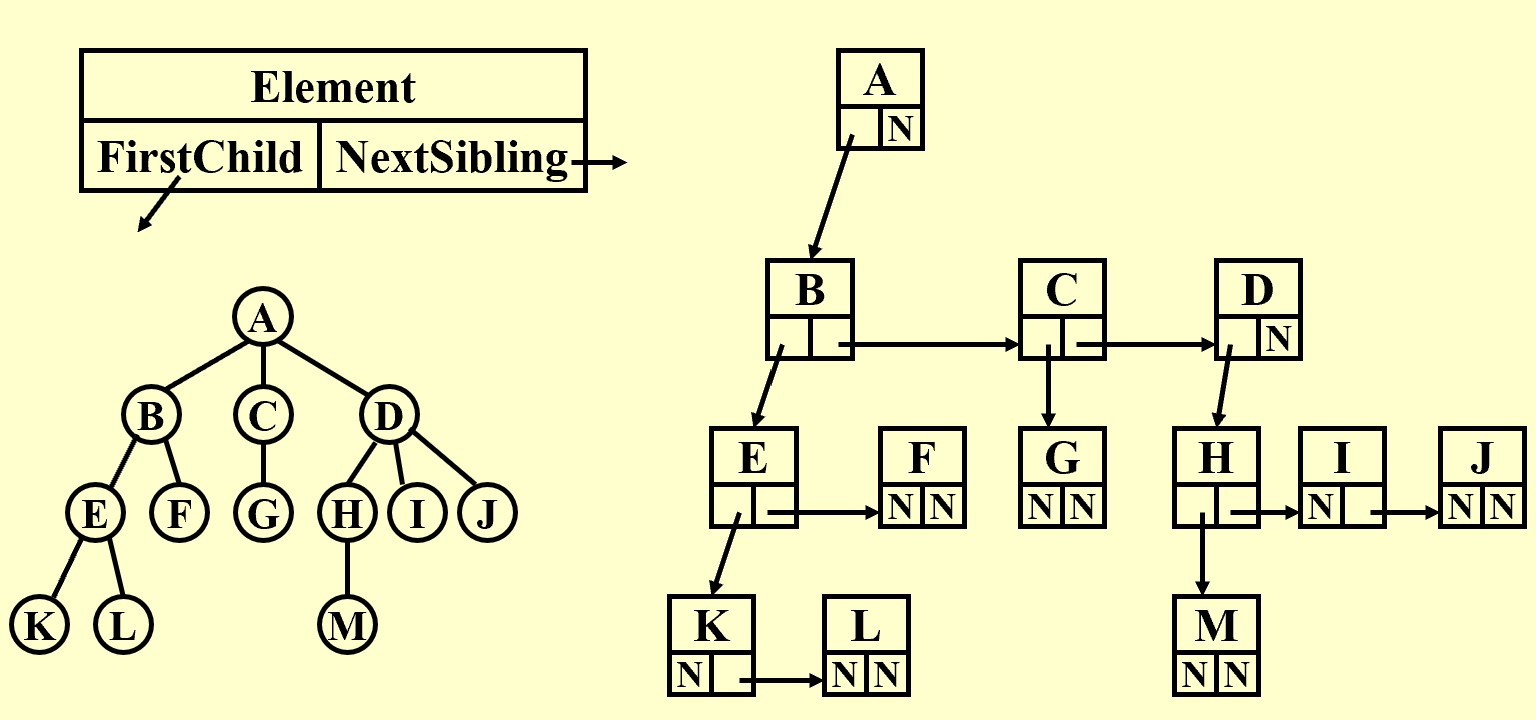
Implementation of a BiTree

Traversal

Example

There is a picture to better understand tree trasval.

Implementation

inorder

preorder

postorder

rebuild

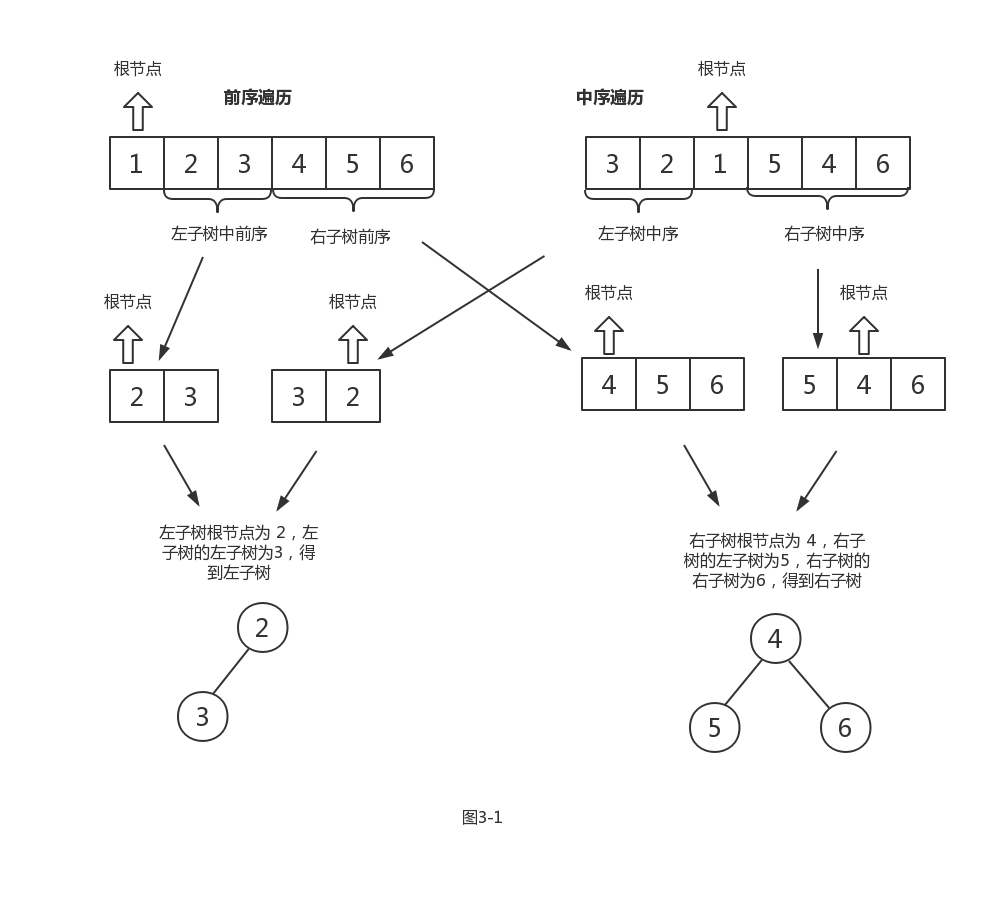
Tree BuildMyTree(int inorder[],int postorder[],int n)
{
    Tree T;
    if(n==0){
        return NULL;
    }
    T=(Tree)malloc(sizeof(BiTree));
    if(n==1){
        T->Element=inorder[0];
        T->Left=NULL;
        T->Right=NULL;
        return T;
    }
    int left;
    int right;
    for(int i=0;i<n;i++){
        if(inorder[i]==postorder[n-1]){
            left=i;
            break;
        }
    }
    right=n-left-1;
    T->Element=postorder[n-1];
    T->Left=BuildMyTree(inorder,postorder,left);
    T->Right=BuildMyTree(inorder+left+1,postorder+left,right);
    return T;
}

Properties of Binary Trees

Threaded BinaryTree

对于没有左或者右孩子的节点，我们根据线索二叉树的不同，让他们分别指向不同的遍历顺序中的前继节点或者后继节点，更大化地利用空间。
对于没有孩子又没有前/后继的节点，其线索为NULL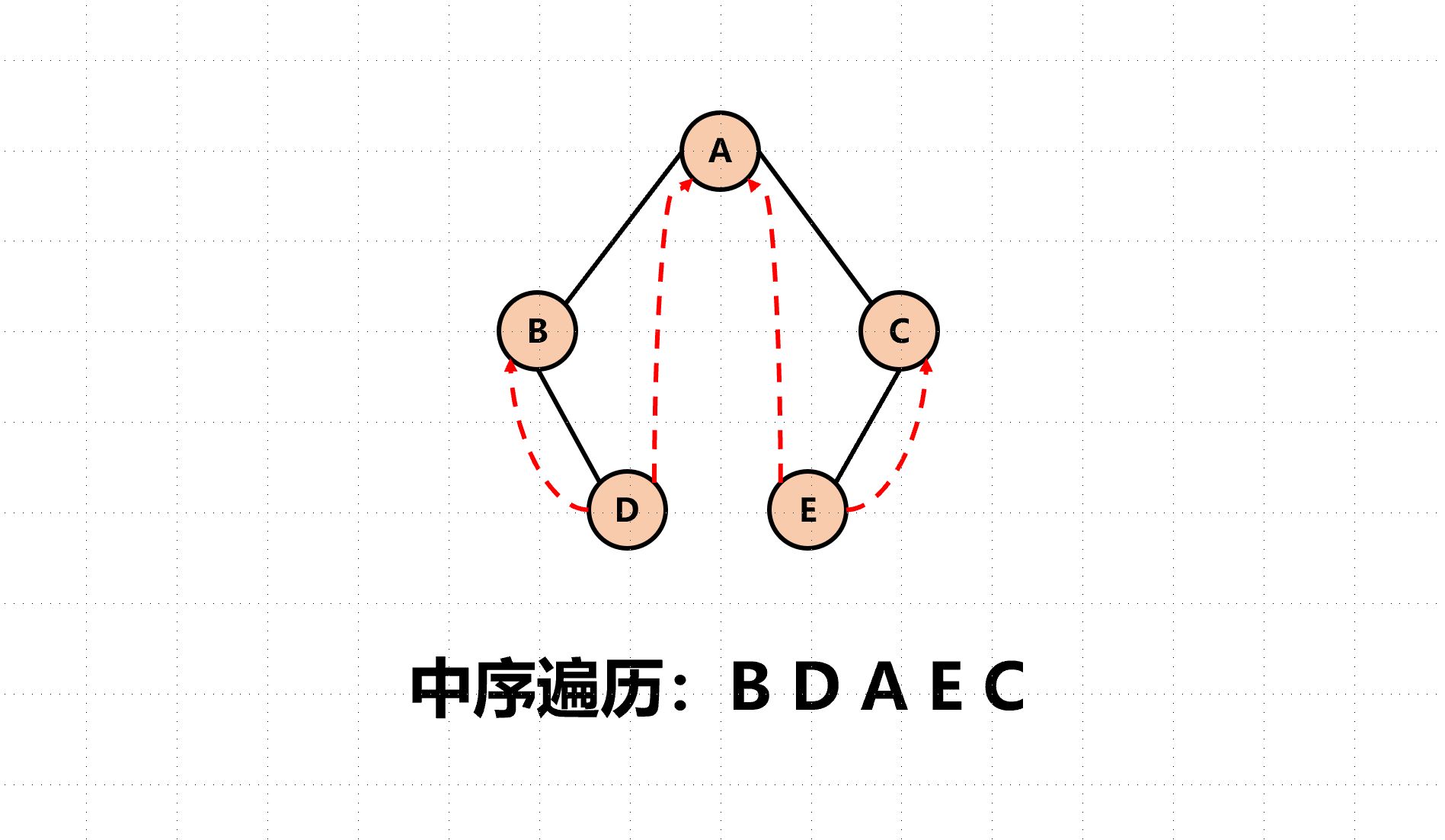

同时，为了知道左右子树到底是不是真的孩子还是线索二叉树的线索，还有两个布尔变量应该在结构体中申明。

Implementation

typedef  struct  ThreadedTreeNode  *PtrTo  ThreadedNode;
typedef  struct  PtrToThreadedNode  ThreadedTree;
typedef  struct  ThreadedTreeNode {
       int LeftThread;   /* if it is TRUE, then Left */
       ThreadedTree Left;      /* is a thread, not a child ptr.   */
       ElementType Element;
       int RightThread; /* if it is TRUE, then Right */
       ThreadedTree Right;    /* is a thread, not a child ptr.   */
}

Binary Search Tree

Definition

【Definition】
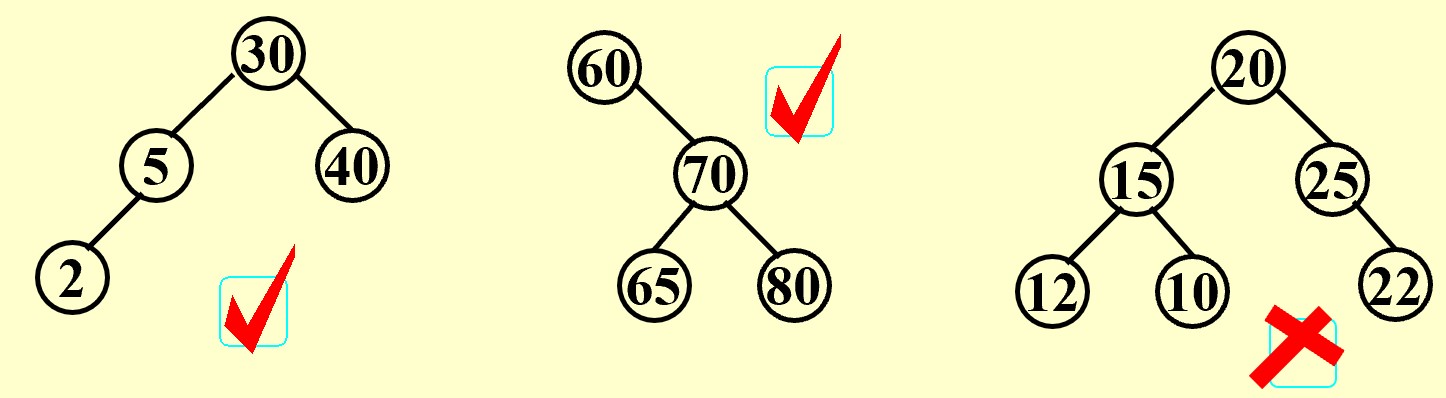
A binary search tree is a binary tree. It may be empty. If it is not empty, it satisfies the following properties:
(1) Every node has a key which is an integer, and the keys are distinct.
(2) The keys in a nonempty left subtree must be smaller than the key in the root of the subtree.
(3) The keys in a nonempty right subtree must be larger than the key in the root of the subtree.
(4) The left and right subtrees are also binary search trees.

Operations & Implementations

Operations

SearchTree  MakeEmpty( SearchTree T ); 
Position  Find( ElementType X, SearchTree T ); 
Position  FindMin( SearchTree T ); 
Position  FindMax( SearchTree T ); 
SearchTree  Insert( ElementType X, SearchTree T ); 
SearchTree  Delete( ElementType X, SearchTree T ); 
ElementType  Retrieve( Position P );

Implementation

Find

Recusive Version

Position  Find( ElementType X,  SearchTree T ) 
{ 
      if ( T == NULL ) 
          return  NULL;  /* not found in an empty tree */
      if ( X < T->Element )  /* if smaller than root */
          return  Find( X, T->Left );  /* search left subtree */
      else 
          if ( X > T->Element )  /* if larger than root */
      return  Find( X, T->Right );  /* search right subtree */
          else   /* if X == root */
      return  T;  /* found */
}

Iterate Version

Position  Iter_Find( ElementType X,  SearchTree T ) 
{ 
      /* iterative version of Find */
      while  ( T )   {
          if  ( X == T->Element )  
    return T ;  /* found */
          if  ( X < T->Element )
             T = T->Left ; /*move down along left path */
          else
     T = T-> Right ; /* move down along right path */
      }  /* end while-loop */
      return  NULL ;   /* not found */
}

FindMin

Position  FindMin( SearchTree T ) 
{ 
      if ( T == NULL )   
          return  NULL; /* not found in an empty tree */
      else 
          if ( T->Left == NULL )   return  T;  /* found left most */
          else   return  FindMin( T->Left );   /* keep moving to left */
}

FindMax

Position  FindMax( SearchTree T ) 
{ 
      if ( T != NULL ) 
          while ( T->Right != NULL )   
            T = T->Right;   /* keep moving to find right most */
      return T;  /* return NULL or the right most */
}

$T(N)=S(N)=d$
where d is the depth of X

Insert

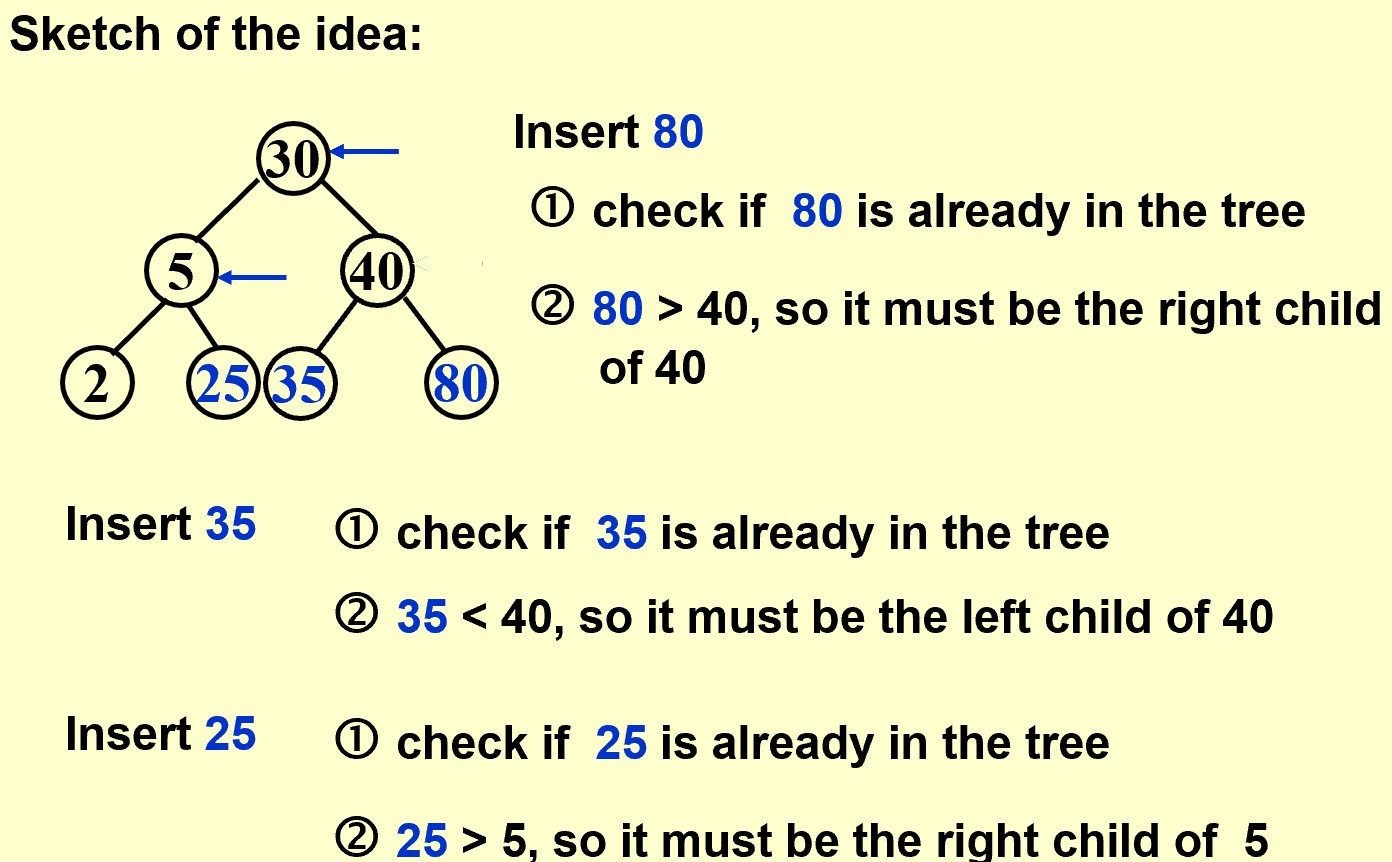
SearchTree Insert( ElementType X, SearchTree T ) 
{ 
      if ( T == NULL ) { /* Create and return a one-node tree */ 
    T = malloc( sizeof( struct TreeNode ) ); 
    if ( T == NULL ) 
       FatalError( "Out of space!!!" ); 
    else { 
       T->Element = X; 
       T->Left = T->Right = NULL; } 
      }  /* End creating a one-node tree */
     else  /* If there is a tree */
     if ( X < T->Element ) 
       T->Left = Insert( X, T->Left ); 
    else 
       if ( X > T->Element ) 
          T->Right = Insert( X, T->Right ); 
       /* Else X is in the tree already; we'll do nothing */ 
    return  T;   /* Do not forget this line!! */ 
}

$T(N)=O(d)$
where d is the depth of X

Delete

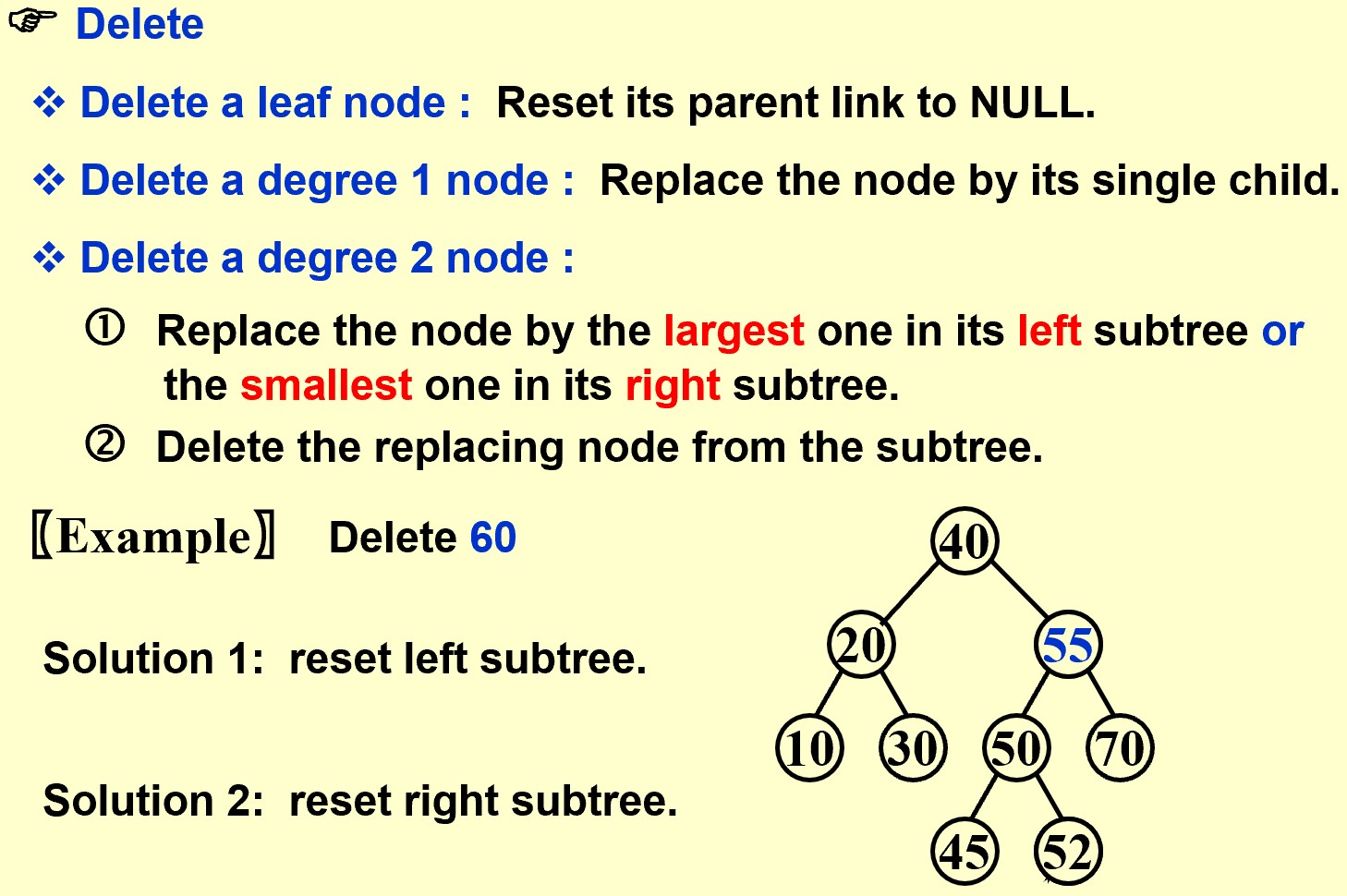
SearchTree  Delete( ElementType X, SearchTree T ) 
{    Position  TmpCell; 
      if ( T == NULL )   Error( "Element not found" ); 
      else  if ( X < T->Element )  /* Go left */ 
        T->Left = Delete( X, T->Left ); 
               else  if ( X > T->Element )  /* Go right */ 
               T->Right = Delete( X, T->Right ); 
             else  /* Found element to be deleted */ 
               if ( T->Left && T->Right ) {  /* Two children */ 
                   /* Replace with smallest in right subtree */ 
                   TmpCell = FindMin( T->Right ); 
                   T->Element = TmpCell->Element; 
                   T->Right = Delete( T->Element, T->Right );  } /* End if */
               else {  /* One or zero child */ 
                   TmpCell = T; 
                   if ( T->Left == NULL ) /* Also handles 0 child */ 
                 T = T->Right; 
                   else  if ( T->Right == NULL )  T = T->Left; 
                   free( TmpCell );  }  /* End else 1 or 0 child */
      return  T; 
}

$T(N) =O(h)$
where h is the height of the tree

Puzzles

Judgment and Choice

There exists a binary tree with 2016 nodes in total, and with 16 nodes having only one child.
F

分析：假设没有孩子的结点(叶结点)个数为n₀，只有一个孩子的结点(度为1的结点)个数为n₁，有两个孩子的结点(度为2的结点)个数为n₂。
则n₀+n₁+n₂=2016 ∵n₀=n₂+1(二叉树的性质：叶结点个数等于度为2的结点个数加1) ∴n₀+n₁+n₂=2016
⇨n₂+1+16+n₂=2016 ⇨2n₂=1999 n₂除不尽，所以答案错误。
公式在课本P118；
树的节点数=所有节点的度数+1
二叉树，叶结点个数等于度为2的结点个数+1
If a general tree T is converted into a binary tree BT, then which of the following BT traversals gives the same sequence as that of the post-order traversal of T?
inorder

转换后，
T的preorder = BT的preorder(preorder不变)
T的postorder = BT的inorder
As the picture showed.

注意:左右子树不同,这棵树的左子树的左子树是空的

Function

6-1 Isomorphic

Two trees, T1 and T2, are isomorphic if T1 can be transformed into T2 by swapping left and right children of (some of the) nodes in T1. For instance, the two trees in Figure 1 are isomorphic because they are the same if the children of A, B, and G, but not the other nodes, are swapped. Give a polynomial time algorithm to decide if two trees are isomorphic.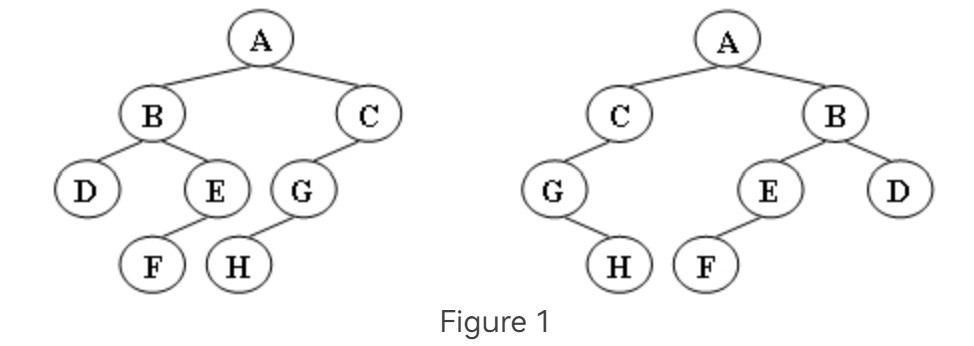

Format of functions:

int Isomorphic( Tree T1, Tree T2 );

where Tree is defined as the following:

typedef struct TreeNode *Tree;
struct TreeNode {
    ElementType Element;
    Tree  Left;
    Tree  Right;
};

The function is supposed to return 1 if T1and T2 are indeed isomorphic, or 0 if not.

Sample program of judge:
#include <stdio.h>
#include <stdlib.h>

typedef char ElementType;

typedef struct TreeNode *Tree;
struct TreeNode {
    ElementType Element;
    Tree  Left;
    Tree  Right;
};

Tree BuildTree(); /* details omitted */

int Isomorphic( Tree T1, Tree T2 );

int main()
{
    Tree T1, T2;
    T1 = BuildTree();
    T2 = BuildTree();
    printf(“%d\n”, Isomorphic(T1, T2));
    return 0;
}

/* Your function will be put here */

Sample Output 1 (for the trees shown in Figure 1):

Sample Output 2 (for the trees shown in Figure 2):

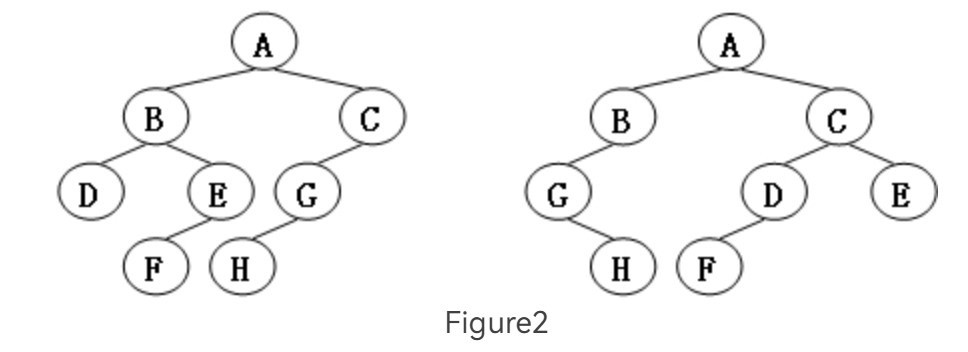
solution

int Isomorphic( Tree T1, Tree T2 )
{
    if(T1==NULL&&T2==NULL)
        return 1;//First Case
    if(T1==NULL&&T2!=NULL)
        return 0;//Breaking Case
    if(T1!=NULL&&T2==NULL)
        return 0;//Breaking Case
    if (T1->Element!=T2->Element)
        return 0;//Breaking Case
    if(T1->Left==NULL&&T2->Left==NULL)
        return Isomorphic(T1->Right,T2->Right);
    if((T1->Left!=NULL&&T2->Left!=NULL)&&(T1->Left->Element==T2->Left->Element))
        return Isomorphic(T1->Left,T2->Left)&&Isomorphic(T1->Right,T2->Right);
    else
        return Isomorphic(T1->Left,T2->Right)&&Isomorphic(T1->Right,T2->Left);
}

Program

7-1 ZigZagging on a Tree

Suppose that all the keys in a binary tree are distinct positive integers. A unique binary tree can be determined by a given pair of postorder and inorder traversal sequences. And it is a simple standard routine to print the numbers in level-order. However, if you think the problem is too simple, then you are too naive. This time you are supposed to print the numbers in “zigzagging order” — that is, starting from the root, print the numbers level-by-level, alternating between left to right and right to left. For example, for the following tree you must output: 1 11 5 8 17 12 20 15.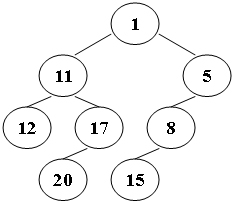

Input Specification:
Each input file contains one test case. For each case, the first line gives a positive integer N (≤30), the total number of nodes in the binary tree. The second line gives the inorder sequence and the third line gives the postorder sequence. All the numbers in a line are separated by a space.

Output Specification:
For each test case, print the zigzagging sequence of the tree in a line. All the numbers in a line must be separated by exactly one space, and there must be no extra space at the end of the line.
Sample Input:

8
12 11 20 17 1 15 8 5
12 20 17 11 15 8 5 1

Sample Output:

1 11 5 8 17 12 20 15

solution

#include<stdio.h>
#include<stdlib.h>

typedef struct BiTree
{
    int Element;
    struct BiTree *Left;
    struct BiTree *Right;
}BiTree,*Tree;


void ZigZaggingorder(Tree root)
{
    Tree Stack1[105];
    Tree Stack2[105];
    int top1=0;
    int top2=0;
    printf("%d",root->Element);
    if(root->Left||root->Right) printf(" ");
    if(root->Right!=NULL) Stack1[++top1]=root->Right;
    if(root->Left!=NULL) Stack1[++top1]=root->Left;
    int flag=-1;
    while (top1||top2)
    {
        if(flag==-1){
            while (top1)
            {
                if(Stack1[top1]->Left!=NULL) Stack2[++top2]=Stack1[top1]->Left;
                if(Stack1[top1]->Right!=NULL) Stack2[++top2]=Stack1[top1]->Right;
                if(top1==1 && top2==0){
                    printf("%d",Stack1[top1]->Element);
                }
                else {
                    printf("%d ",Stack1[top1]->Element);
                }
                top1--;
            }
            flag*=-1;
        }
        if(flag==1){
            while (top2)
            {
                if(Stack2[top2]->Right!=NULL) Stack1[++top1]=Stack2[top2]->Right;
                if(Stack2[top2]->Left!=NULL) Stack1[++top1]=Stack2[top2]->Left;
                if(top1==0 && top2==1){
                    printf("%d",Stack2[top2]->Element);
                }
                else {
                    printf("%d ",Stack2[top2]->Element);
                }
                top2--;
            }
            flag*=-1;
        }
    }
}

Tree BuildMyTree(int inorder[],int postorder[],int n)
{
    Tree T;
    if(n==0){
        return NULL;
    }
    T=(Tree)malloc(sizeof(BiTree));
    if(n==1){
        T->Element=inorder[0];
        T->Left=NULL;
        T->Right=NULL;
        return T;
    }
    int left;
    int right;
    for(int i=0;i<n;i++){
        if(inorder[i]==postorder[n-1]){
            left=i;
            break;
        }
    }
    right=n-left-1;
    T->Element=postorder[n-1];
    T->Left=BuildMyTree(inorder,postorder,left);
    T->Right=BuildMyTree(inorder+left+1,postorder+left,right);
    return T;
}

int main(){
    int n;
    int inorder[105];
    int postorder[105];
    Tree T;
    scanf("%d",&n);
    for(int i=0;i<n;i++){
        scanf("%d",&inorder[i]);
    }
    for(int i=0;i<n;i++){
        scanf("%d",&postorder[i]);
    }
    // printf("%d",inorder[0]);
    // printf("%d",postorder[0]);
    T=BuildMyTree(inorder,postorder,n);
    ZigZaggingorder(T);
    //levelorder(T);
    return 0;
}

Union & Find

Relation

Symmetric

Relation is symmetric, If $(a, b) ∈ R$, then $(b, a) ∈ R$.

Transitive

Relation is transitive, If $(a, b) ∈ R$ & $(b, c) ∈ R$, then $(a, c) ∈ R$.

Relflexive

Relation is relflexive, If $(a, a) ∈ R$.

Consistent

Relation is symmetric and relflexive.

Implementation

Array Data Stucture Implementation

S [element] = the element’s parent
S [root] = -SetSize and set name = root's index

Union

void  SetUnion ( DisjSet S, SetType Rt1,SetType Rt2 )
{
    S[Rt2] = Rt1;     
}

Find (Including Path Compression)

Recursive Version

SetType  Find ( ElementType  X, DisjSet  S )
{
    if ( S[ X ] <= 0 )
        return  X;
    else    
        return  S[ X ] = Find( S[ X ], S );
}

Iterate Version

SetType  Find ( ElementType  X, DisjSet  S )
{   ElementType  root,  trail,  lead;
    for ( root = X; S[ root ] > 0; root = S[ root ] );  /* find the root */
    for ( trail = X; trail != root; trail = lead ) {
       lead = S[ trail ] ;   
       S[ trail ] = root ;   
    }  /* 重复再找一次，找的时候把每一层根的最终根都改掉 */
    return  root ;
}

SetUnion By Size

void SetUnion(int X1,int X2)
{
    int root1=Find(X1);
    int root2=Find(X2);
    if(root1==root2)
    {
        S[root2]=root1;
        root1-=root2;
    }
    else
    {
        if(root1<root2)//root1 is bigger than root2,so we Union root2 to root1
        {
            S[root2]=root1;
            root1-=root2;//update the value of root2
        }
        else
        {
            S[root1]=root2;
            root2-=root1;
        }
    }
}

Puzzles

Judgement & Choice

In Union/Find algorithm, if Unions are done by size, the depth of any node must be no more than $N/2$, but not $O(logN)$.
F

每做一次归并，都会使得小的集合深度加1，但是总的深度还是看大的集合。只有深度相同的归并才能使得总的深度加1，2,2归并，深度变为3；3,3归并深度变为4。因此深度最大为$log_{2}N+1$
所以，N次归并和M次查找，复杂度为$O(N+M\log_2N)$
The array representation of a disjoint set containing numbers 0 to 8 is given by { 1, -4, 1, 1, -3, 4, 4, 8, -2 }. Then to union the two sets which contain 6 and 8 (with union-by-size), the index of the resulting root and the value stored at the root are:
B.4 and -5

正的数代表根，负的数代表最终根以及集合的元素个数。没合并前是{0，1，2，3}，{4，5，6}，{7，8}

Program
7-1 File Transfer
We have a network of computers and a list of bi-directional connections. Each of these connections allows a file transfer from one computer to another. Is it possible to send a file from any computer on the network to any other?
Input Specification:
Each input file contains one test case. For each test case, the first line contains $N (2≤N≤10^4)$, the total number of computers in a network. Each computer in the network is then represented by a positive integer between 1 and N. Then in the following lines, the input is given in the format:
I c1 c2
where I stands for inputting a connection between c1 and c2;
or
C c1 c2
where C stands for checking if it is possible to transfer files between c1 and c2;
or
S
where S stands for stopping this case.

Output Specification:
For each C case, print in one line the word “yes” or “no” if it is possible or impossible to transfer files between c1 and c2, respectively. At the end of each case, print in one line “The network is connected.” if there is a path between any pair of computers; or “There are k components.” where k is the number of connected components in this network.

Sample Input 1:

Sample Output 1:

no
no
yes
There are 2 components.

Sample Input 2:

Sample Output 2:

no
no
yes
yes
The network is connected.

Solution

#include<stdio.h>


int Find ( int X, int S[] )
{ 
    int root, trail, lead;
    for ( root = X; S[root] > 0; root = S[root] ); /* find the root */
    for ( trail = X; trail != root; trail = lead ) {
       lead = S[trail] ;   
       S[trail] = root ;   
    }/* collapsing */
    return  root ;
}

void SetUnion(int S[],int X1,int X2)
{
    int root1=Find(X1,S);
    int root2=Find(X2,S);
    if(root1==root2)
    {
        S[root2]=root1;
        root1-=root2;
    }
    else
    {
        if(root1<root2)//root1 is bigger than root2,so we Union root2 to root1
        {
            S[root2]=root1;
            root1-=root2;//update the value of root2
        }
        else
        {
            S[root1]=root2;
            root2-=root1;
        }
    }
}

int main(){
    int n;
    int a,b=0;
    int cnt[10010];
    scanf("%d",&n);
    int computer[10010];
    for(int i=0;i<10010;i++){
        computer[i]=-1;
    }
    char c = 'O';
    while(c!='S'){
        scanf("%c",&c);
        if(c=='I'){
            scanf("%d",&a);
            scanf("%d",&b);
            SetUnion(computer,a,b);
        }
        if(c=='C'){
            scanf("%d",&a);
            scanf("%d",&b);
            if(Find(a,computer)==Find(b,computer)){
                printf("yes\n");
            }
            if(Find(a,computer)!=Find(b,computer)){
                printf("no\n");
            }
        }
    }
    int flag=0;
    for(int i=1;i<=n;i++){
        if(computer[i]<0){
            flag++;
        }
    }
    if(flag==1){
         printf("The network is connected.");
    }
    else{
        printf("There are %d components.\n",flag);
    }
    return 0;
}

Graph

Definitions

$G( V, E )$ where $G$ ::= graph,
$V = V( G )$ ::= finite nonempty set of vertices,
and $E = E( G )$ ::= finite set of edges.
Undirected graph: $( vi , vj ) = ( vj , vi )$ ::= the same edge.
Directed graph (digraph): $< v_i , v_j > ::= v_i -> v_j \neq < vj , vi >$
In this class,Restrictions :
(1) Self loop is illegal.
(2) Multigraph is not considered
(Multigraph: A Graph that there could be more than one edge between two nodes)
Complete graph: a graph that has the maximum number of edges

Simple Implementation of Graph

Adjacency Matrix

adj_mat[n][n] is defined for $G(V, E)$ with $n$ vertices, $n > 1$ :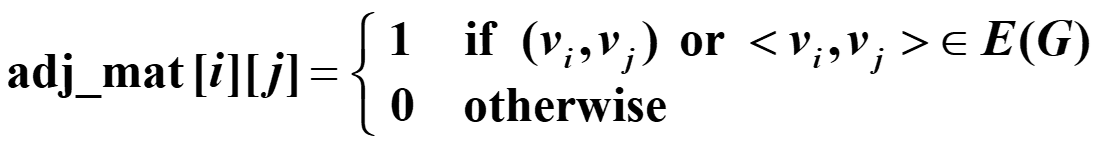

Note: If G is undirected, then adj_mat[ ][ ] is symmetric.
Thus we can save space by storing only half of the matrix.
In a word, the advantage of adjacency matrix is simple to implement, but the disadvantage is waste of space. In praxtice,for most incomplete graphs, more than half of the space is often wasted.

Adjacency Lists

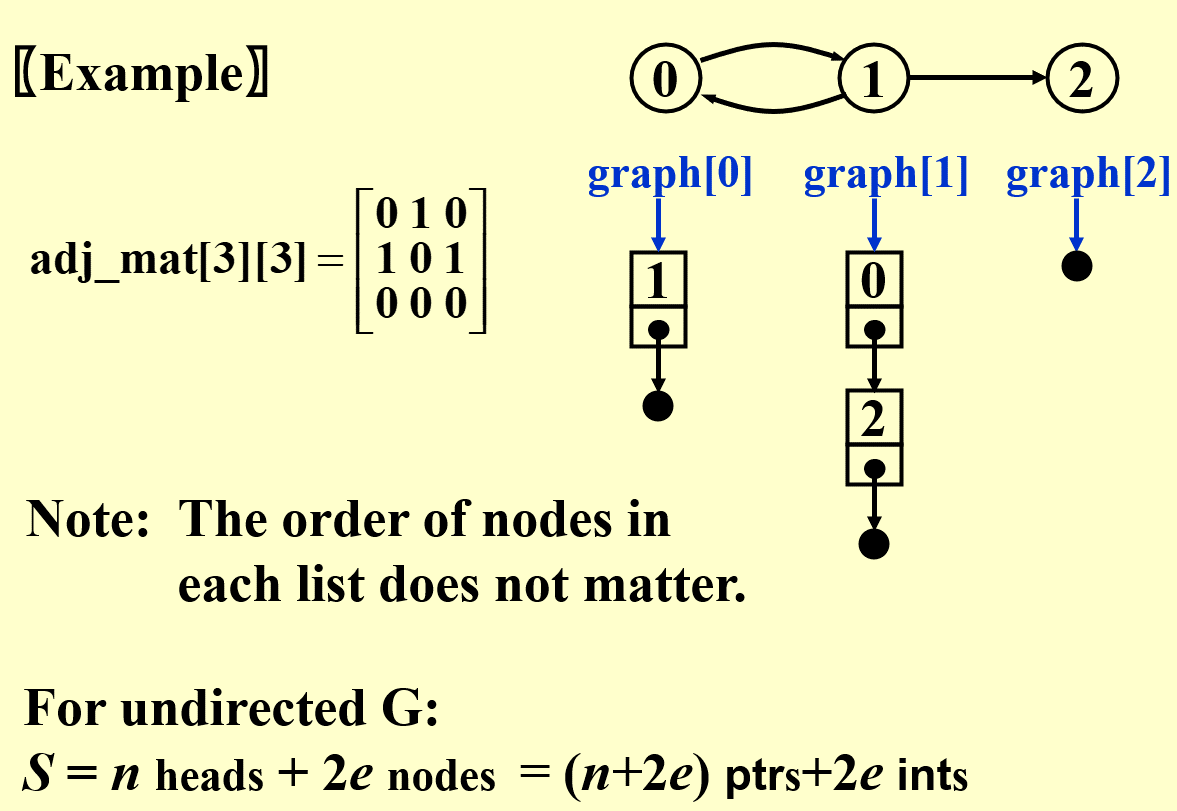
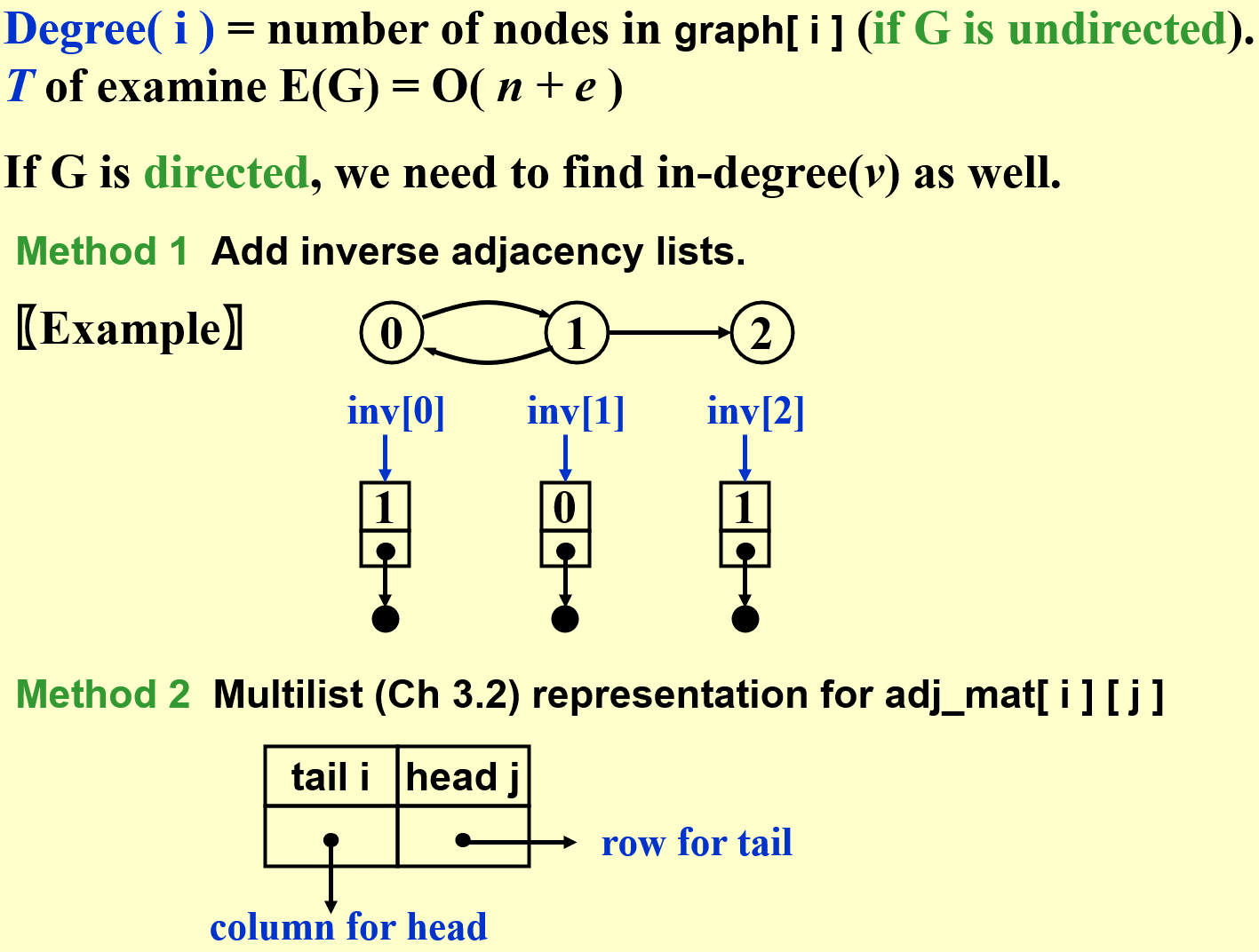
Simple Implementation in C

typedef int Vertex;         /* 用顶点下标表示顶点,为整型 */
typedef int WeightType;        /* 边的权值设为整型 */
typedef char DataType;        /* 顶点存储的数据类型设为字符型 */

/* 边的定义 */
typedef struct ENode *PtrToENode;
struct ENode{
    Vertex V1, V2;      /* 有向边<V1, V2> */
    WeightType Weight;  /* 权重 */
};
typedef PtrToENode Edge;

/* 邻接点的定义 */
typedef struct AdjVNode *PtrToAdjVNode; 
struct AdjVNode{
    Vertex AdjV;        /* 邻接点下标 */
    WeightType Weight;  /* 边权重 */
    PtrToAdjVNode Next;    /* 指向下一个邻接点的指针 */
};

/* 顶点表头结点的定义 */
typedef struct Vnode{
    PtrToAdjVNode FirstEdge;/* 边表头指针 */
    DataType Data;            /* 存顶点的数据 */
    /* 注意：很多情况下，顶点无数据，此时Data可以不用出现 */
} AdjList[MaxVertexNum];    /* AdjList是邻接表类型 */

/* 图结点的定义 */
typedef struct GNode *PtrToGNode;
struct GNode{  
    int Nv;     /* 顶点数 */
    int Ne;     /* 边数   */
    AdjList G;  /* 邻接表 */
};
typedef PtrToGNode LGraph; /* 以邻接表方式存储的图类型 */

LGraph CreateGraph( int VertexNum )
{ /* 初始化一个有VertexNum个顶点但没有边的图 */
    Vertex V;
    LGraph Graph;

    Graph = (LGraph)malloc( sizeof(struct GNode) ); /* 建立图 */
    Graph->Nv = VertexNum;
    Graph->Ne = 0;
    /* 初始化邻接表头指针 */
    /* 注意：这里默认顶点编号从0开始，到(Graph->Nv - 1) */
       for (V=0; V<Graph->Nv; V++){
            Graph->G[V].FirstEdge = NULL;
       }
    return Graph; 
}

void InsertEdge( LGraph Graph, Edge E )
{
    PtrToAdjVNode NewNode;

    /* 插入边 <V1, V2> */
    /* 为V2建立新的邻接点 */
    NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
    NewNode->AdjV = E->V2;
    NewNode->Weight = E->Weight;
    /* 将V2插入V1的表头 */
    NewNode->Next = Graph->G[E->V1].FirstEdge;
    Graph->G[E->V1].FirstEdge = NewNode;

    /* 若是无向图，还要插入边 <V2, V1> */
    /* 为V1建立新的邻接点 */
    NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
    NewNode->AdjV = E->V1;
    NewNode->Weight = E->Weight;
    /* 将V1插入V2的表头 */
    NewNode->Next = Graph->G[E->V2].FirstEdge;
    Graph->G[E->V2].FirstEdge = NewNode;
}

LGraph BuildGraph()
{
    LGraph Graph;
    Edge E;
    Vertex V;
    int Nv, i;

    scanf("%d", &Nv);   /* 读入顶点个数 */
    Graph = CreateGraph(Nv); /* 初始化有Nv个顶点但没有边的图 */ 

    scanf("%d", &(Graph->Ne));   /* 读入边数 */
    if ( Graph->Ne != 0 ) { /* 如果有边 */ 
        E = (Edge)malloc( sizeof(struct ENode) ); /* 建立边结点 */ 
        /* 读入边，格式为"起点 终点 权重"，插入邻接矩阵 */
        for (i=0; i<Graph->Ne; i++) {
            scanf("%d %d %d", &E->V1, &E->V2, &E->Weight); 
            /* 注意：如果权重不是整型，Weight的读入格式要改 */
            InsertEdge( Graph, E );
        }
    } 

    /* 如果顶点有数据的话，读入数据 */
    for (V=0; V<Graph->Nv; V++) {
        scanf(" %c", &(Graph->G[V].Data));
    }
    return Graph;
}

Toplogical Sort

Definition

AOV Network ::= digraph $G$ in which $V( G )$ represents activities ( e.g. the courses ) and $E( G )$ represents precedence relations ( e.g. means that C1 is a prerequisite course of C3 ).
$i$ is a predecessor of $j$ ::= there is a path from $i$ to $j$
$i$ is an immediate predecessor of $j ::= < i$, $j > \in E( G )$,then $j$ is called a successor ( immediate successor ) of $i$
Partial order ::= a precedence relation which is both transitive $( i \to k, k \to j \Rightarrow i \to j )$ and irreflexive ( $i \to i$ is impossible ).
(which means there must be no circles)
A topological order is a linear ordering of the vertices of a graph such that, for any two vertices, $i, j,$ if $i$ is a predecessor of $j$ in the network then $i$ precedes $j$ in the linear ordering.

Normal Implementation

void Topsort( Graph G )
{   int  Counter;
    Vertex  V, W;
    for ( Counter = 0; Counter < NumVertex; Counter ++ ) {
        V = FindNewVertexOfDegreeZero( );
        if ( V == NotAVertex ) {
            Error ( “Graph has a cycle” );   break;  }
        TopNum[ V ] = Counter; /* or output V */
        for ( each W adjacent to V ){
                Indegree[ W ] – – ;
        }
    }
}

Analyse the time complexity:$T = O( |V|^2 )$

Implementation with Queue

void Topsort( Graph G )
{   
    Queue  Q;
    int  Counter = 0;
    Vertex  V, W;
    Q = CreateQueue( NumVertex );
    MakeEmpty( Q );
    for ( each vertex V )
    if ( Indegree[ V ] == 0 ){
        Enqueue( V, Q );
    }
    while ( !IsEmpty( Q ) ) {
        V = Dequeue( Q );
        TopNum[ V ] = ++ Counter; /* assign next */
        for ( each W adjacent to V ){
            if ( – – Indegree[ W ] == 0 ) {
                Enqueue( W, Q );
            }
        }
    }  /* end-while */
    if ( Counter != NumVertex ){
        Error( “Graph has a cycle” );
    }
    DisposeQueue( Q ); /* free memory */
}

Analyse the time complexity:$T = O( |V|+|E| )$

Shortest Path

Given a digraph $G = ( V, E )$, and a cost function $c( e )$ for $e \in E( G )$. The length of a path $P$ from source to destination is $\sum_{e_i \in P}c(e_i)$ (also called weighted path length).

Simple representation

Table[ i ].Dist ::= distance from s to vi  /* initialized to be $\infin$ except for s */
Table[ i ].Known ::= 1 if vi is checked; or 0 if not
Table[ i ].Path ::= for tracking the path   /* initialized to be 0 *,上一个点/

Implementation

Unweighted Graph with a Queue

void Unweighted( Table T )
{   /* T is initialized with the source vertex S given */
    Queue  Q;
    Vertex  V, W;
    Q = CreateQueue (NumVertex );  
    MakeEmpty( Q );
    Enqueue( S, Q ); /* Enqueue the source vertex */
    while ( !IsEmpty( Q ) ) {
        V = Dequeue( Q );
        T[ V ].Known = true; /* not really necessary */
        for ( each W adjacent to V ){
            if ( T[ W ].Dist == Infinity ) {
                T[ W ].Dist = T[ V ].Dist + 1;
                T[ W ].Path = V;
                Enqueue( W, Q );
            } /* end-if Dist == Infinity */
        }
    } /* end-while */
    DisposeQueue( Q ); /* free memory */
}

$T = O( |V|+|E| )$

Dijkstra’s Algorithm for Weighted Graph

void Dijkstra( Table T )
{   /* T is initialized by Figure 9.30 on p.303 */
    Vertex  V, W;
    for ( ; ; ) {
        V = smallest unknown distance vertex;
        if ( V == NotAVertex ){
            break; 
        }
        T[ V ].Known = true;
        for ( each W adjacent to V ){
            if ( !T[ W ].Known ){
                if ( T[ V ].Dist + Cvw < T[ W ].Dist ) {
                    Decrease( T[ W ].Dist  to T[ V ].Dist + Cvw );
                    T[ W ].Path = V;
                } /* end-if update W */
                //Cvw: the weight of the edge form v to w
            }
        }
    } /* end-for( ; ; ) */
}

NOTE:This algorithm does not work for edge with negative cost.
$T = O( |V|^2 + |E| )$
If this algorithm work with a priority queue,the time complexity could be
$T = O( |V| log|V| + |E| log|V| ) = O( |E| log|V| )$

Acyclic Graphs

If the graph is acyclic, vertices may be selected in topological order since when a vertex is selected, its distance can no longer be lowered without any incoming edges from unknown nodes.

Network Flow Problem

$G=(V,E)$是一个有向图，其中每条边$(u,v)∈E$均有一个非负容量$c(u,v)>=0$。如果$(u,v) \notin E$，则假定$c(u,v)=0$。流网络中有两个特别的顶点：源点$s$和汇点$t$。下图展示了一个流网络的实例。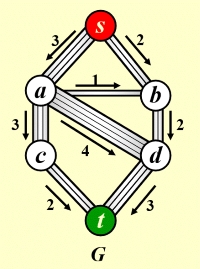

Minimum Spanning Tree

A spanning tree of a graph $G$ is a tree which consists of $V( G )$ and a subset of $E( G )$

Note:

The minimum spanning tree is a tree since it is acyclic — the number of edges is $|V| – 1$.
It is minimum for the total cost of edges is minimized.
It is spanning because it covers every vertex.
A minimum spanning tree exists iff $G$ is connected.
Adding a non-tree edge to a spanning tree, we obtain a cycle

Prim’s Algorithm

对顶点操作，在最小生成树的顶点集$U$和待处理顶点集$V-U$中，不断地寻找最短边(代价最小边)，找到后将对应顶点加入集合$U$，直到所有顶点均处理完毕($V-U$里没有剩余顶点),DFS

Prim算法如何保证不成环？因为每次选择的点都是在集合$V$以外的

Implementation

/* 邻接矩阵存储 - Prim最小生成树算法 */

Vertex FindMinDist( MGraph Graph, WeightType dist[] )
{ /* 返回未被收录顶点中dist最小者 */
    Vertex MinV, V;
    WeightType MinDist = INFINITY;

    for (V=0; V<Graph->Nv; V++) {
        if ( dist[V]!=0 && dist[V]<MinDist) {
            /* 若V未被收录，且dist[V]更小 */
            MinDist = dist[V]; /* 更新最小距离 */
            MinV = V; /* 更新对应顶点 */
        }
    }
    if (MinDist < INFINITY) /* 若找到最小dist */
        return MinV; /* 返回对应的顶点下标 */
    else return ERROR;  /* 若这样的顶点不存在，返回-1作为标记 */
}

int Prim( MGraph Graph, LGraph MST )
{ /* 将最小生成树保存为邻接表存储的图MST，返回最小权重和 */
    WeightType dist[MaxVertexNum], TotalWeight;
    Vertex parent[MaxVertexNum], V, W;
    int VCount;
    Edge E;

    /* 初始化。默认初始点下标是0 */
    for (V=0; V<Graph->Nv; V++) {
        /* 这里假设若V到W没有直接的边，则Graph->G[V][W]定义为INFINITY */
           dist[V] = Graph->G[0][V];
           parent[V] = 0; /* 暂且定义所有顶点的父结点都是初始点0 */ 
    }
    TotalWeight = 0; /* 初始化权重和     */
    VCount = 0;      /* 初始化收录的顶点数 */
    /* 创建包含所有顶点但没有边的图。注意用邻接表版本 */
    MST = CreateGraph(Graph->Nv);
    E = (Edge)malloc( sizeof(struct ENode) ); /* 建立空的边结点 */

    /* 将初始点0收录进MST */
    dist[0] = 0;
    VCount ++;
    parent[0] = -1; /* 当前树根是0 */

    while (1) {
        V = FindMinDist( Graph, dist );
        /* V = 未被收录顶点中dist最小者 */
        if ( V==ERROR ) /* 若这样的V不存在 */
            break;   /* 算法结束 */

        /* 将V及相应的边<parent[V], V>收录进MST */
        E->V1 = parent[V];
        E->V2 = V;
        E->Weight = dist[V];
        InsertEdge( MST, E );
        TotalWeight += dist[V];
        dist[V] = 0;
        VCount++;

        for( W=0; W<Graph->Nv; W++ ) /* 对图中的每个顶点W */
            if ( dist[W]!=0 && Graph->G[V][W]<INFINITY ) {
            /* 若W是V的邻接点并且未被收录 */
                if ( Graph->G[V][W] < dist[W] ) {
                /* 若收录V使得dist[W]变小 */
                    dist[W] = Graph->G[V][W]; /* 更新dist[W] */
                    parent[W] = V; /* 更新树 */
                }
            }
    } /* while结束*/
    if ( VCount < Graph->Nv ) /* MST中收的顶点不到|V|个 */
       TotalWeight = ERROR;
    return TotalWeight;   /* 算法执行完毕，返回最小权重和或错误标记 */

Kruskal’s Algorithm

对边操作，每次选取一条最短边，如果不会和当前最小生成树构成环（回路），将此最短边加入最小生成树中。当选取了$n-1$（顶点数-1）条边，或找出了所有符合条件的不成环边最小生成树生成完毕,BFS

void Kruskal ( Graph G )
{   T = { } ;
    while  ( T contains less than |V| - 1 edges && E is not empty ) {
        choose a least cost edge (v, w) from E ;
        delete (v, w) from E ;
        if  ( (v, w) does not create a cycle in T )     
            add (v, w) to T ;
        else     
            discard (v, w) ;
    }
    if  ( T contains fewer than |V| - 1 edges )
        Error ( “No spanning tree” ) ;
}

Analysis:$T=O(|E|log|E|)$

Implementation

/* 邻接表存储 - Kruskal最小生成树算法 */

/*-------------------- 顶点并查集定义 --------------------*/
typedef Vertex ElementType; /* 默认元素可以用非负整数表示 */
typedef Vertex SetName;     /* 默认用根结点的下标作为集合名称 */
typedef ElementType SetType[MaxVertexNum]; /* 假设集合元素下标从0开始 */

void InitializeVSet( SetType S, int N )
{ /* 初始化并查集 */
    ElementType X;

    for ( X=0; X<N; X++ ) S[X] = -1;
}

void Union( SetType S, SetName Root1, SetName Root2 )
{ /* 这里默认Root1和Root2是不同集合的根结点 */
    /* 保证小集合并入大集合 */
    if ( S[Root2] < S[Root1] ) { /* 如果集合2比较大 */
        S[Root2] += S[Root1];     /* 集合1并入集合2  */
        S[Root1] = Root2;
    }
    else {                         /* 如果集合1比较大 */
        S[Root1] += S[Root2];     /* 集合2并入集合1  */
        S[Root2] = Root1;
    }
}

SetName Find( SetType S, ElementType X )
{ /* 默认集合元素全部初始化为-1 */
    if ( S[X] < 0 ) /* 找到集合的根 */
        return X;
    else
        return S[X] = Find( S, S[X] ); /* 路径压缩 */
}

bool CheckCycle( SetType VSet, Vertex V1, Vertex V2 )
{ /* 检查连接V1和V2的边是否在现有的最小生成树子集中构成回路 */
    Vertex Root1, Root2;

    Root1 = Find( VSet, V1 ); /* 得到V1所属的连通集名称 */
    Root2 = Find( VSet, V2 ); /* 得到V2所属的连通集名称 */

    if( Root1==Root2 ) /* 若V1和V2已经连通，则该边不能要 */
        return false;
    else { /* 否则该边可以被收集，同时将V1和V2并入同一连通集 */
        Union( VSet, Root1, Root2 );
        return true;
    }
}
/*-------------------- 并查集定义结束 --------------------*/

/*-------------------- 边的最小堆定义 --------------------*/
void PercDown( Edge ESet, int p, int N )
{ /* 改编代码4.24的PercDown( MaxHeap H, int p )    */
  /* 将N个元素的边数组中以ESet[p]为根的子堆调整为关于Weight的最小堆 */
    int Parent, Child;
    struct ENode X;

    X = ESet[p]; /* 取出根结点存放的值 */
    for( Parent=p; (Parent*2+1)<N; Parent=Child ) {
        Child = Parent * 2 + 1;
        if( (Child!=N-1) && (ESet[Child].Weight>ESet[Child+1].Weight) )
            Child++;  /* Child指向左右子结点的较小者 */
        if( X.Weight <= ESet[Child].Weight ) break; /* 找到了合适位置 */
        else  /* 下滤X */
            ESet[Parent] = ESet[Child];
    }
    ESet[Parent] = X;
}

void InitializeESet( LGraph Graph, Edge ESet )
{ /* 将图的边存入数组ESet，并且初始化为最小堆 */
    Vertex V;
    PtrToAdjVNode W;
    int ECount;

    /* 将图的边存入数组ESet */
    ECount = 0;
    for ( V=0; V<Graph->Nv; V++ )
        for ( W=Graph->G[V].FirstEdge; W; W=W->Next )
            if ( V < W->AdjV ) { /* 避免重复录入无向图的边，只收V1<V2的边 */
                ESet[ECount].V1 = V;
                ESet[ECount].V2 = W->AdjV;
                ESet[ECount++].Weight = W->Weight;
            }
    /* 初始化为最小堆 */
    for ( ECount=Graph->Ne/2; ECount>=0; ECount-- )
        PercDown( ESet, ECount, Graph->Ne );
}

int GetEdge( Edge ESet, int CurrentSize )
{ /* 给定当前堆的大小CurrentSize，将当前最小边位置弹出并调整堆 */

    /* 将最小边与当前堆的最后一个位置的边交换 */
    Swap( &ESet[0], &ESet[CurrentSize-1]);
    /* 将剩下的边继续调整成最小堆 */
    PercDown( ESet, 0, CurrentSize-1 );

    return CurrentSize-1; /* 返回最小边所在位置 */
}
/*-------------------- 最小堆定义结束 --------------------*/


int Kruskal( LGraph Graph, LGraph MST )
{ /* 将最小生成树保存为邻接表存储的图MST，返回最小权重和 */
    WeightType TotalWeight;
    int ECount, NextEdge;
    SetType VSet; /* 顶点数组 */
    Edge ESet;    /* 边数组 */

    InitializeVSet( VSet, Graph->Nv ); /* 初始化顶点并查集 */
    ESet = (Edge)malloc( sizeof(struct ENode)*Graph->Ne );
    InitializeESet( Graph, ESet ); /* 初始化边的最小堆 */
    /* 创建包含所有顶点但没有边的图。注意用邻接表版本 */
    MST = CreateGraph(Graph->Nv);
    TotalWeight = 0; /* 初始化权重和     */
    ECount = 0;      /* 初始化收录的边数 */

    NextEdge = Graph->Ne; /* 原始边集的规模 */
    while ( ECount < Graph->Nv-1 ) {  /* 当收集的边不足以构成树时 */
        NextEdge = GetEdge( ESet, NextEdge ); /* 从边集中得到最小边的位置 */
        if (NextEdge < 0) /* 边集已空 */
            break;
        /* 如果该边的加入不构成回路，即两端结点不属于同一连通集 */
        if ( CheckCycle( VSet, ESet[NextEdge].V1, ESet[NextEdge].V2 )==true ) {
            /* 将该边插入MST */
            InsertEdge( MST, ESet+NextEdge );
            TotalWeight += ESet[NextEdge].Weight; /* 累计权重 */
            ECount++; /* 生成树中边数加1 */
        }
    }
    if ( ECount < Graph->Nv-1 )
        TotalWeight = -1; /* 设置错误标记，表示生成树不存在 */

    return TotalWeight;
}

Depth-First Search(DFS)

Implementatiom

void DFS ( Vertex V )  /* this is only a template */
{   visited[ V ] = true;  /* mark this vertex to avoid cycles */
    for ( each W adjacent to V )
        if ( !visited[ W ] )
    DFS( W );
} /* T = O( |E| + |V| ) as long as adjacency lists are used */

Application 1: List Components

void ListComponents ( Graph G ) 
{   for ( each V in G ) 
        if ( !visited[ V ] ) {
    DFS( V );
               printf(“\n“);
        }
}

Application 2: Biconnectivity

【Definition】
articulation point: $v$ is an articulation point if $G’ = DeleteVertex( G, v )$ has at least 2 connected components.
biconnected graph: $G$ is a biconnected graph if $G$ is connected and has no articulation points.
biconnected component: A biconnected component is a maximal biconnected subgraph.
Now, we want to find the biconnected components of a connected undirected $G$.

Solution:
Find the articulation points in $G$:

The root is an articulation point if it has at least 2 children
Any other vertex $u$ is an articulation point if $u$ has at least 1 child, and it is impossible to move down at least 1 step and then jump up to u’s ancestor,which means that :$u$ is not the root, and has at least 1 child such that $Low( child ) \geq Num( u )$.

$Num(u)$:DFS遍历时顶点的序号
$Low(u)$:原图中和该顶点有边的顶点的最低序号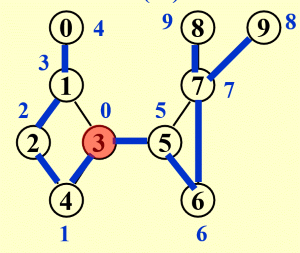

In this graph,vertices {1，3，5，7} are articulation point.

Implementation in C

#define min(x,y) ((x)>(y)?(y):(x))
void DFS(int u, Graph G, void(*visit)(Vertex V)){
    num[u]=low[u]=count++;
    stack[++top] = u;
    instack[u]=true;

    for(PtrToVNode v =G->Array[u];v;v=v->Next){
        //和G相邻的点
        if (!instack[v->Vert] && !visited[v->Vert]) {
            DFS(v->Vert, G, visit);
            //v->Vert:v的节点编号
            low[u] = min(low[u], low[v->Vert]);
        }
        else if (instack[v->Vert]) {
            low[u] = min(low[u], num[v->Vert]);
        }
    }

    Vertex poped_v = -1;
    if (num[u] == low[u]) {
        while (poped_v != u) {
            poped_v=stack[top--];
            visit(poped_v);
            instack[poped_v] = false;
            visited[poped_v] = true;
        }
        printf("\n");
    }

}

Application 3: Euler Circuits

【Definition】

Euler tour: Draw each line exactly once without lifting your pen from the paper.
Euler curcuit: Draw each line exactly once without lifting your pen from the paper, AND finish at the starting point.

【Proposition】

An Euler circuit is possible only if the graph is connected and each vertex has an even degree.
An Euler tour is possible if there are exactly two vertices having odd degree. One must start at one of the odd-degree vertices.

Puzzles

Judgement & Choice

Program

Sort

Inseration Sort

Implementation

void InsertionSort ( ElementType A[ ], int N ) 
{ 
      int  j, P; 
      ElementType  Tmp; 

      for ( P = 1; P < N; P++ ) { 
    Tmp = A[ P ];  /* the next coming card */
    for ( j = P; j > 0 && A[ j - 1 ] > Tmp; j-- ) 
          A[ j ] = A[ j - 1 ]; 
          /* shift sorted cards to provide a position 
                       for the new coming card */
    A[ j ] = Tmp;  /* place the new card at the proper position */
      }  /* end for-P-loop */
}

Analysis

The worst case:Input A[ ] is in reverse order. $T( N ) = O( N^2 )$

The best case:Input A[ ] is in sorted order. $T( N ) = O( N )$

Shell Sort

Implementation

void Shellsort( ElementType A[ ], int N ) 
{ 
      int  i, j, Increment; 
      ElementType  Tmp; 
      for ( Increment = N / 2; Increment > 0; Increment /= 2 )  
    /*h sequence */
    for ( i = Increment; i < N; i++ ) { /* insertion sort */
          Tmp = A[ i ]; 
          for ( j = i; j >= Increment; j - = Increment ) 
        if( Tmp < A[ j - Increment ] ) 
              A[ j ] = A[ j - Increment ]; 
        else 
              break; 
        A[ j ] = Tmp; 
    } /* end for-I and for-Increment loops */
}

Heap Sort

Implementation

void PercDown(int A[], int N, int p) {
    int parent, child;
    int temp = A[p];
    for (parent = p; 2 * parent + 1 < N; parent = child) {
        child = 2 * parent + 1;
        if (child + 1 < N && A[child + 1] > A[child])
            child++;
        if (temp < A[child])
            A[parent] = A[child];
        else
            break;
    }
    A[parent] = temp;
}

void Heapsort( ElementType A[ ], int N ) 
{  int i; 
    for ( i = N / 2; i >= 0; i - - ) /* BuildHeap */ 
        PercDown( A, i, N ); 
    for ( i = N - 1; i > 0; i - - ) { 
        Swap( &A[ 0 ], &A[ i ] ); /* DeleteMax */ 
        PercDown( A, 0, i ); 
    } 
}

QuickSort(Median-3 version)

Implementation

#define Cutoff 5
/*小数据下插入排序更快，不足Cutoff用插入排序*/

void  Quicksort( ElementType A[ ], int N ) 
{ 
    Qsort( A, 0, N - 1 ); 
    /* A:     the array     */
    /* 0:     Left index     */
    /* N – 1: Right index    */
}//面向对象思想，封装过程

/* Return median of Left, Center, and Right */ 
/* Order these and hide the pivot */ 
ElementType Median3( ElementType A[ ], int Left, int Right ) 
{ 
    int  Center = ( Left + Right ) / 2; 
    if ( A[ Left ] > A[ Center ] ) 
        Swap( &A[ Left ], &A[ Center ] ); 
    if ( A[ Left ] > A[ Right ] ) 
        Swap( &A[ Left ], &A[ Right ] ); 
    if ( A[ Center ] > A[ Right ] ) 
        Swap( &A[ Center ], &A[ Right ] ); 
    /* Invariant: A[ Left ] <= A[ Center ] <= A[ Right ] */ 
    Swap( &A[ Center ], &A[ Right - 1 ] ); /* Hide pivot */ 
    /* only need to sort A[ Left + 1 ] … A[ Right – 2 ] */
    return  A[ Right - 1 ];  /* Return pivot */ 
}

void  Qsort( ElementType A[ ], int Left, int Right ) 
{   
    int  i,  j; 
    ElementType  Pivot; 
    if ( Left + Cutoff <= Right ) {  /* if the sequence is not too short */
            Pivot = Median3( A, Left, Right );  /* select pivot */
            i = Left;     j = Right – 1;  /* why not set Left+1 and Right-2? */
        for( ; ; ) { 
            while ( A[ + +i ] < Pivot ) { }  /* scan from left */
            while ( A[ – –j ] > Pivot ) { }  /* scan from right */
            if ( i < j ) 
                Swap( &A[ i ], &A[ j ] );  /* adjust partition */
            else break;  /* partition done */
        }
            Swap( &A[ i ], &A[ Right - 1 ] ); /* restore pivot */ 
            Qsort( A, Left, i - 1 );      /* recursively sort left part */
            Qsort( A, i + 1, Right );   /* recursively sort right part */
        }  /* end if - the sequence is long */
    else /* do an insertion sort on the short subarray */ 
            InsertionSort( A + Left, Right - Left + 1 );
    }

Complexity and Stability

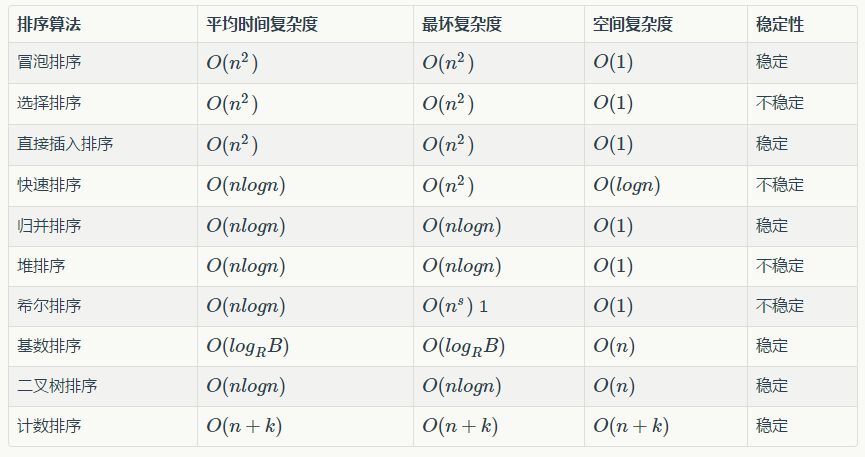
Puzzles

Judgment and Choice

During the sorting, processing every element which is not yet at its final position is called a “run”. Which of the following cannot be the result after the second run of quicksort?
A.5, 2, 16, 12, 28, 60, 32, 72
B.2, 16, 5, 28, 12, 60, 32, 72
C.2, 12, 16, 5, 28, 32, 72, 60
D.5, 2, 12, 28, 16, 32, 72, 60
D

三个pivot , 快速排序每一轮的过程, 观察有几个元素在正确的位置, 每轮当分割点pivot的元素一定会在正确的位置。最理想的是每次都选到中间值, 这样两轮后有三个分割点。
A选项，28和72在正确位置, B选项，2和72在正确位置。他们是因为选到了最值72,所以是两个pivot。C选择2和28,32在正确位置。D选项，没有选到最值, 又没有三个pivot, 就是错的。
Given input { 321, 156, 57, 46, 28, 7, 331, 33, 34, 63 }. Which one of the following is the result after the 2nd run of the Least Signification Digit (LSD) radix sort?
A.→7→321→28→34→33→331→156→46→57→63
B.→7→321→28→331→34→33→46→156→57→63
C.→156→28→321→331→33→34→46→57→63→7
D.→7→321→28→331→33→34→46→156→57→63
D

第一次按照个位排：321->331->33->63->34->156->46->57->7->28
第二次按照十位排：7->321->28->331->33->34->46->156->57->63
Among the following sorting methods, which ones will be slowed down if we store the elements in a linked structure instead of a sequential structure?
Insertion sort; 2. Selection Sort; 3. Bubble sort; 4. Shell sort; 5. Heap sort
A.1 and 2 only
B.2 and 3 only
C.3 and 4 only
D.4 and 5 only
D

如果在链表中存储数据，变慢的操作是：访问第 $n$ 个元素，变快的是插入。shell需要访问第 $k$ 个元素，heap需要访问 $i/2$ 的元素。

Hashing

Symbol Table

Definition

e.g.
In a symbol table for a compiler
name = identifier (e.g. int)
attribute = a list of lines that use the identifier, and some other fields

这里先说一下哈希表的定义：哈希表是一种根据关键码去寻找值的数据映射结构，该结构通过把关键码映射的位置去寻找存放值的地方，说起来可能感觉有点复杂，我想我举个例子你就会明白了，最典型的的例子就是字典，大家估计小学的时候也用过不少新华字典吧，如果我想要获取“按”字详细信息，我肯定会去根据拼音an去查找拼音索引(当然也可以是偏旁索引)，我们首先去查an在字典的位置，查了一下得到“安”，结果如下。这过程就是键码映射，在公式里面，就是通过key去查找f(key)。其中，按就是关键字(key)，f()就是字典索引，也就是哈希函数，查到的页码4就是哈希值。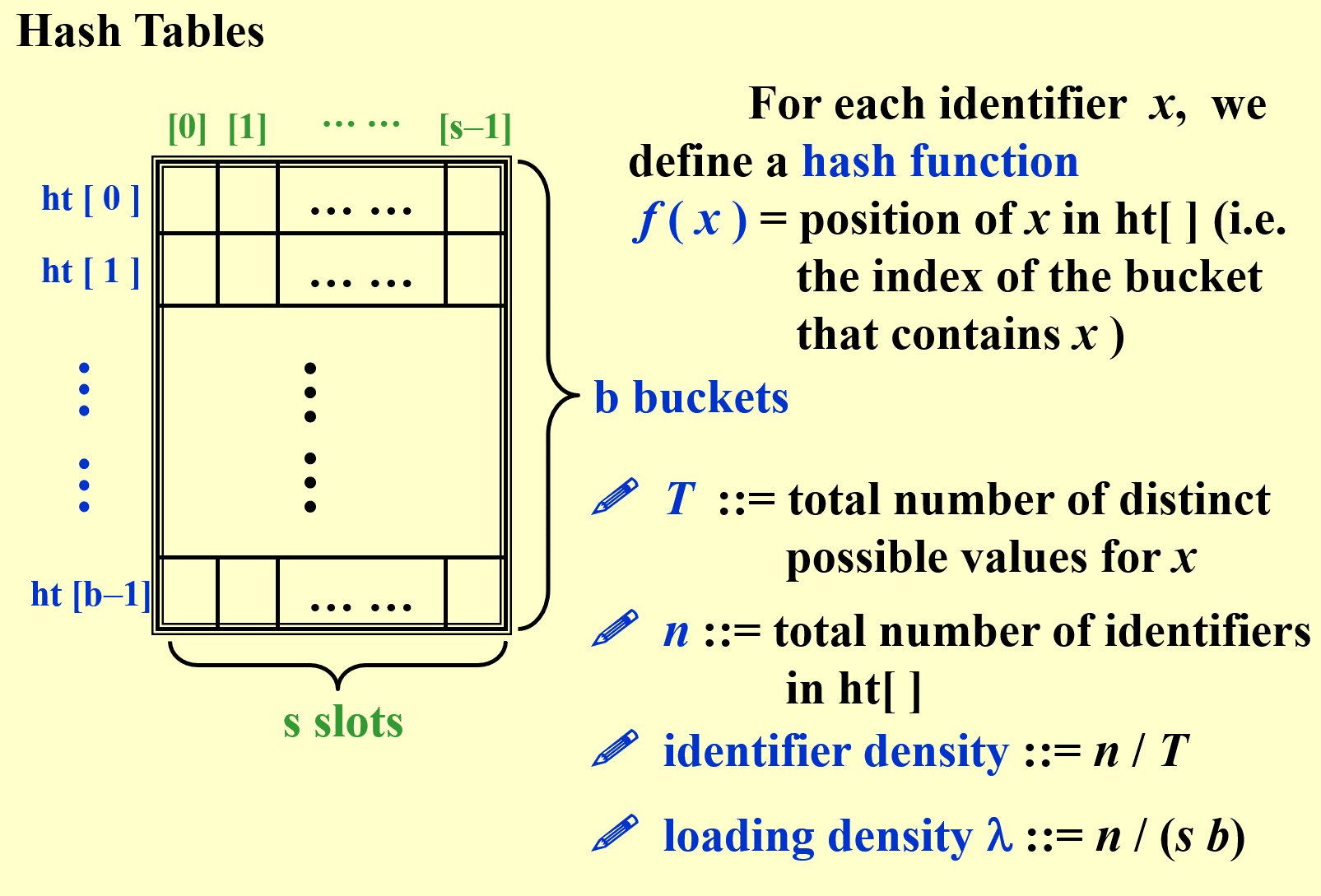

细分T和key
T：key的值域
n：实际的key的数量

Collision & Overflow

A collision occurs when we hash two nonidentical identifiers into the same bucket, i.e. $f ( i1 ) = f ( i2 )$ when $i1 \neq i2$ .
但是问题又来了，我们要查的是“按”，而不是“安，但是他们的拼音都是一样的。也就是通过关键字按和关键字安可以映射到一样的字典页码4的位置，这就是哈希冲突(也叫哈希碰撞)，在公式上表达就是key1≠key2，但f(key1)=f(key2)。冲突会给查找带来麻烦，你想想，你本来查找的是“按”，但是却找到“安”字，你又得向后翻一两页，在计算机里面也是一样道理的。

An overflow occurs when we hash a new identifier into a full bucket.

Hash Function

$f ( x )$ must be easy to compute and minimizes the number of collisions.
$f ( x )$ should be unbiased. That is, for any x and any i, we have that Probability$( f ( x ) = i ) = 1 / b$. Such kind of a hash function is called a uniform hash function.

Implementation

Struct Definition

struct  ListNode; 
typedef  struct  ListNode  *Position; 
struct  HashTbl; 
typedef  struct  HashTbl  *HashTable; 
struct  ListNode { 
    ElementType  Element; 
    Position  Next; 
}; 
typedef  Position  List; 
/* List *TheList will be an array of lists, allocated later */ 
/* The lists use headers (for simplicity), */ 
/* though this wastes space */ 
struct  HashTbl { 
    int  TableSize; 
    List  *TheLists; 
};

Create Table

HashTable  InitializeTable( int TableSize ) 
{   HashTable  H; 
    int  i; 
    if ( TableSize < MinTableSize ) { 
        Error( "Table size too small" );  return NULL;  
    } 
    H = malloc( sizeof( struct HashTbl ) );  /* Allocate table */
    if ( H == NULL )    FatalError( "Out of space!!!" ); 
    H->TableSize = NextPrime( TableSize );  /* Better be prime */
    H->TheLists = malloc( sizeof( List ) * H->TableSize );  /*Array of lists*/
    if ( H->TheLists == NULL )   FatalError( "Out of space!!!" ); 
    for( i = 0; i < H->TableSize; i++ ) {   /* Allocate list headers */
    H->TheLists[ i ] = malloc( sizeof( struct ListNode ) ); /* Slow! */
    if ( H->TheLists[ i ] == NULL )  FatalError( "Out of space!!!" ); 
    else    H->TheLists[ i ]->Next = NULL;
    } 
    return  H; 
}

Find

Position  Find ( ElementType Key, HashTable H ) 
{ 
    Position P; 
    List L; 

    L = H->TheLists[ Hash( Key, H->TableSize ) ]; 

    P = L->Next; 
    while( P != NULL && P->Element != Key )  /* Probably need strcmp */ 
    P = P->Next; 
    return P; 
}

Insertion

void  Insert ( ElementType Key, HashTable H ) 
{ 
    Position   Pos, NewCell; 
    List  L; 
    Pos = Find( Key, H ); 
    if ( Pos == NULL ) {   /* Key is not found, then insert */
        NewCell = malloc( sizeof( struct ListNode ) ); 
        if ( NewCell == NULL )     FatalError( "Out of space!!!" ); 
        else { 
            L = H->TheLists[ Hash( Key, H->TableSize ) ]; 
            NewCell->Next = L->Next; 
            NewCell->Element = Key; /* Probably need strcpy! */ 
            L->Next = NewCell; 
        } 
    } 
}

Separate Chaining

使用链接散列表。这个是使用链表解决冲突。表的长度由题目给定。

Open Adressing

Algorithm: insert key into an array of hash table
{
    index = hash(key);
    initialize i = 0// the counter of probing;
    while ( collision at index ) {
    index = ( hash(key) + f(i) ) % TableSize;
    if ( table is full )    break;
    else    i ++;
    }
    if ( table is full )
    ERROR (“No space left”);
    else
    insert key at index;
}

$f(x)$:Collision resolving function.$f(0) = 0.$

Liner Probing

$f(i) = i$

Quadratic Probing

$f ( i ) = i^2 $
【Theorem】
If quadratic probing is used, and the table size is prime, then a new element can always be inserted if the table is at least half empty.
【Proof】
Just prove that the first $[TableSize/2]$ alternative locations are all distinct.
That is, for any
$0 < i \neq j < [TableSize/2]$, we have
$( h(x) + i^2 )\% TableSize \neq ( h(x) + j^2 ) \% TableSize $
Suppose: $ h(x) + i^2 = h(x) + j^2 ( mod \ TableSize )$
then:
$i^2 = j^2 ( mod \ TableSize )$
$( i + j ) ( i - j ) = 0 (mod \ TableSize )$

BUT as TableSize is prime,either $( i + j )$ or $( i - j )$ is divisible by TableSize!
Contradiction !
Q.E.D.

Implementation in Quadratic Probing

Find

Position  Find ( ElementType Key, HashTable H ) 
{   Position  CurrentPos; 
    int  CollisionNum; 
    CollisionNum = 0; 
    CurrentPos = Hash( Key, H->TableSize ); 
    while( H->TheCells[ CurrentPos ].Info != Empty && 
    H->TheCells[ CurrentPos ].Element != Key ) 
    { 
        CurrentPos += 2 * ++CollisionNum - 1; 
        //(i+1)^2-i^2=2*(i+1)-1
        if ( CurrentPos >= H->TableSize )  CurrentPos - = H->TableSize; 
    } 
    return CurrentPos; 
}

Insertion

void  Insert ( ElementType Key, HashTable H ) 
{ 
    Position  Pos; 
    Pos = Find( Key, H ); 
    if ( H->TheCells[ Pos ].Info != Legitimate ) { /* OK to insert here */ 
    H->TheCells[ Pos ].Info = Legitimate; 
    H->TheCells[ Pos ].Element = Key; /* Probably need strcpy */ 
    } 
}

Double Hashing

Rehashing

动态增长哈希表

Build another table that is about twice as big;(find the closest prime to the two times big size)
Scan down the entire original hash table for non-deleted elements;
Use a new function to hash those elements into the new table.

When to Rehash?

As soon as the table is half full
When an insertion fails
When the table reaches a certain load factor

Usually there should have been $N/2$ insertions before rehash, so $O(N)$ rehash only adds a constant cost to each insertion.
However, in an interactive system, the unfortunate user whose insertion caused a rehash could see a slowdown.

通过第一个$hash_1(x)$计算，比如
$hash_1(x)=key\%TableSize$,若此时出现冲突，使用如下的公式计算
$(hash_1(key) + i * hash_2(key)) \% TableSize $。
还有冲突就增加$i$。

Algorithm Anlysis

Space Comlexity

Time Comlexity

List

Abustrct Data Type

Linked List

Interfaces

Stack & Queue

Stack

Definition

Operations & Implementations

Operations:

Array Implementation:

Linked List Implemetation(with Dummy):

Applications

Balance Symbols

Postfix Infix Prefix Evaluation

Queue

Definition

Operations & Implementations

Operations:

Implementations:

Circular Queue:

Complete Binary Tree and Heap

Operations and Implementations

Binary Heap

Definition

Array Representation

MinHeap & MaxHeap

Implementations

Initialize

Insert

DeleteMin

PercolateUp & PercolateDown

Puzzles

Judgment and Choice

Program

7-1 Pop Sequence

Tree

Definition

Implementation

Turn to BiTree

Implementation of a BiTree

Traversal

Example

Implementation

inorder

preorder

postorder

rebuild

Properties of Binary Trees

Threaded BinaryTree

Implementation

Binary Search Tree

Definition

Operations & Implementations

Operations

Implementation

Find

Insert

Delete

Puzzles

Judgment and Choice

Function

6-1 Isomorphic

Program

7-1 ZigZagging on a Tree

Union & Find

Relation

Symmetric

Transitive

Relflexive

Consistent

Implementation

Array Data Stucture Implementation

Union

Find (Including Path Compression)

SetUnion By Size

Puzzles

Judgement & Choice